Also available : French version
Essentials before you start
This page is written in basic HTML. No plug-ins are required to view this page. You can save the molecule file with
the right mouse button. You will be able to see the molecule without connection with a visualization
program like RasMol.
In order to view molecular structures on line you will have to configure your browser and to acquire CHIME plug-in.
Introduction
More information : click HERE
The molecular constitution is all of the atoms linked with bonds. In the Lewis formula the bonds are represented with a dash between the two bonded atoms and a lone electron pair with a dash on the considered atom. The molecular geometrical shape is the arrangement of these atoms in the space. A lot of physical or chemical properties are the consequence of particular geometrical shape. In this chapter we are going to study the geometrical shape for some molecules or ions. We'll only see the simple cases where we can distinguish without ambiguity a central atom (noted A) and its peripheral atoms (noted X). We won't study molecules with a central atom which belongs to transition elements.
Experimental results
SO2 is very more soluble in water than CO2. This difference of behaviour in the macroscopic scale is explained in the microscopic scale by the geometrical shape of these molecules. CO2 and SO2 have each other two oxygen atoms bonded to a central atom. The IR spectrum shows that CO2 is linear whereas SO2 is triangular. So, the dipolar moment of SO2 is not equal to zero and this molecule can act with H2O, whereas the dipolar moment of CO2 is equal to zero because of the compensation of the dipolar moments of bonds.
A lot of physical and chemical methods determinate the molecular geometrical shape : RX, electronic and neutronic diffraction, UV, IR, Raman, microwave spectroscopy. RMN and RPE also permit to obtain precious information notably in the dynamic molecular estate. At the present time, we know with precision the bond lenghts and the angles between bonds for a lot of molecules. One of the important aspects for geometrical shape is to explain and to forsee this shape for selected molecules
Principles of the VSEPR method
Origin
In 1957 the canadian chemist R.J Gillespie (university Mc
Master Hamilton, Ontario) took back british N.
Sigdwick and H. Powell idea, and developped the theory of the valence shell electron pair repulsion VSEPR.
This method prolongs in the geometrical shape aspect the description of the chemical bond by G. N. Lewis (1916).
The electrons in the valence shell of most stable molecules and ions are paired (some rare molecules like NO2 have unpaired electrons). The Pauli principle shows that only the electrons which own opposite spin quantic numbers move in the same space region, because they are described by the same orbital. These electrons can be grouped together in pairs. In the Lewis model, the bond between two atoms is described by a bonding electron pair. The electron pairs no employed in a bond are lone pairs or non bonding electron pair. Afterwards X indicate an atom attached to the central atom A and E a non-bonding pair on the central atom. In first approximation, mutiple bonds are treated like a single bond with only one shared pairs
|
|
Atoms attached to A : X |
Non-bonding pair on A : E |
|
Number |
n |
m |
Basic principle
The first approximation of the theory is to liken electron pairs to ponctual electric charges.
Each pair which belongs to the valence shell moves to a comparable distance from the atom center, so on the same sphere whose the center
is the atom A. On this sphere, the position of the pairs is the consequence of their mutual
repulsions. Although this is not an electrostatic interaction between ponctual charges (because the behaviour of electrons are governed
by quantum mechanics) we obtain a correct result if we search the arrangement that gives maximum distances between electron pairs.
At this first level of approximation, we don't distinguich bonding and non bonding electron pairs. In these conditions, the arrangement that
minimizes the pair repulsions depends only the sum (m + n), and so, if we stop at the number six, we see these following geometrical
figures.
|
m + n |
Overall geometry |
|
2 |
Linear |
|
3 |
Trigonal |
|
4 |
Tetrahedral |
|
5 |
Trigonal bipyramidal |
|
6 |
Octahedral |
For these five geometrical figures, we'll see more arrangements of the electron pairs. We'll see molecules with single or multiple bonds.
The different arrangement of pairs
Linear arrangement
For example, molecules with simple bonds :
![]()
Beryllium, an element of the second column of the periodic classification, has for electronical configuration : [He] 2s2. It has two single bonds with two atoms in BeCl2.
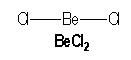
|
AX2 |
For example, molecules with multiple bonds :

|
AX2 |
AX2 |
AX2 |
Exercise : draw the Lewis structure for the following molecules and verify their family and geometrical shape.
|
AX2 |
Trigonal arrangement
We distinguish two families :
|
AX3 |
AX2E |
|
Trigonal planar |
Bent |
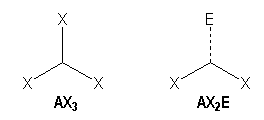
For example, molecules with single bonds :
|
B |
Sn |
|
[He] 2s2 2p1 |
[Kr] 4d10 5s2 5p2 |
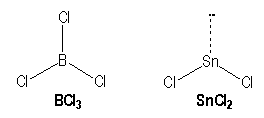
|
AX3 |
AX2E |
Molecules with multiple bonds :
|
S |
O |
N |
|
[Ne] 3s2 3p4 |
[He] 2s2 2p4 |
[He] 2s2 2p3 |
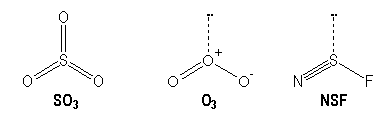
|
AX3 |
AX2E |
AX2E |
Exercise : draw the Lewis structure for the following molecules and ions and verifiy their family and geometrical shape.
|
AX3 |
AX2E |
Tetrahedral
We distinguish three families :
|
AX4 |
AX3E |
AX2E2 |
|
Tetrahedral |
Trigonal pyramidal |
Bent |
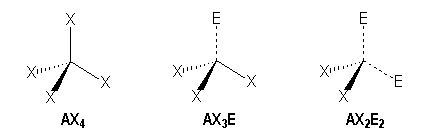
For example molecules with simple bonds :
|
Si |
P |
O |
|
[Ne] 3s2 3p2 |
[Ne] 3s2 3p3 |
[He] 2s2 2p4 |
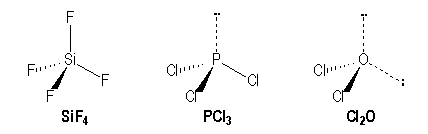
|
AX4 |
AX3E |
AX2E2 |
For example molecules with multiple bonds :
|
P |
S |
|
[Ne] 3s2 3p1 |
[Ne] 3s2 3p4 |
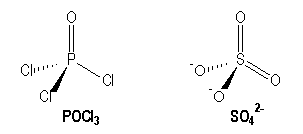
|
AX4 |
AX4 |
Exercise : draw the Lewis structure for the following molecules and ions. Verify their family and geometrical shape.
|
AX4 |
AX3E |
AX2E2 |
Trigonal bipyramidal
The corners of the bipyramid aren't equivalent. We can split in axial (a) or equatorial (e) corners.

The problem can be resolve if we refine the hypothesis of the method. The non bonding and bonding pairs can be differently treated, indeed the position in the space of bonding pairs is controled by the field of the two bonding atoms, but the position of non bonding pairs is controled by only one atom : the central atom. And so, the volum of a non bonding E is higher than this of bonding S. The repulsion between pairs follows the order :
E-E (x) > E-S (y) > S-S (z)
A practical parameter to assess the importance of the repulsion between the pairs is the angle a between the directions of these pairs. This parameter allow to compare the energies of the two arrangements (1) and (2) when we count the interactions with the previous inegalities. If we only count the interactions when a £ 90° (we disregard the other one) we obtain :
|
Arrangement (1) |
Arrangement (2) |
|
The pair E acts with 2 atomes X |
The pair E acts with 3 atomes X |
The first arrangement is stabler than the second. The molecules
that belong to this first arrangement, are called "disphenoïd" molecules, like SF4.
Experimentally we don't know stereoisomer for this molecule.
A same study for the other possible trigonal bipyramidal shapes, shows that the lone pairs must preferably occupy the equatorial positions.
|
AX5 |
AX4E |
AX3E2 |
AX2E3 |
|
Trigonal bipyramidal |
Seesaw |
T-shaped |
Linear |
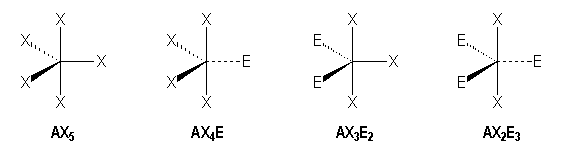
For example molecules with single bonds :
|
P |
S |
Cl |
I |
|
[Ne] 3s2 3p3 |
[Ne] 3s2 3p4 |
[Ne] 3s2 3p5 |
[Kr] 4 d10 5s2 5p5 |
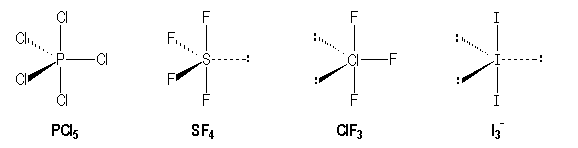
|
AX5 |
AX4E |
AX3E |
AX2E3 |
Molecules and ions with multiple bonds :
|
S |
I |
|
[Ne] 3s2 3p4 |
[Kr] 4 d105s2 5p5 |
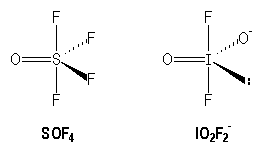
|
AX5 |
AX4E | |
Exercise : draw the Lewis structure for these following molecules or ions, and verify their family and geometrical shape.
|
AX5 |
AX4E |
Octahedral arrangement
We observe these families :
|
AX6 |
AX5E |
AX4E2 |
|
Octahedral |
Square pyramidal |
Square planar |
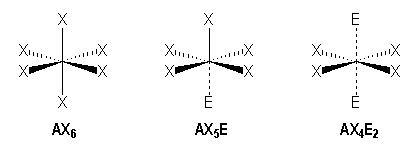
For example, molecules with single bonds :
|
S |
Br |
I |
|
[Ne] 3s2 3p4 |
[Kr] 3 d10 4s2 4p5 |
[Kr] 4 d10 5s2 5p5 |
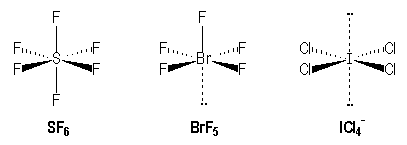
|
AX6 |
AX5E |
AX4E2 |
Molecules with multiple bonds :
|
I |
Xe |
|
[Kr] 4 d10 5s2 5p5 |
[Kr] 4 d10 5s2 5p6 |
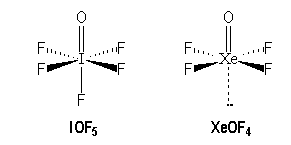
|
AX6 |
AX5E |
Second order effects
|
109,5° |
107° |
104,5° |
We observe the same evolution for the ionic derivatives of NH3 :
|
NH4+ |
NH3 |
NH2- |
|
109,5° |
107° |
104° |
For example in the trigonal arrangement, the molecules like HCHO and COCl2 have an angle between single bonds inferior to 120°.
|
115,8° |
111,3° |
In the tetraedric arrangement we observe a diminution of the angle between single bonds when in this order the central atom owns only single bonds, one double bond and one triple bond like in : SiF4, POF3 and NSF3.
|
109,5° |
102° |
98° |
In the trigonal bipyramidal arrangement the angle FOF is inferior to 120° in SOF4.
|
110° |
Influence of the difference of electronegativity between atoms
There are two cases :
The first appears when for a same central atom we compare the angles between bonds with atoms X whose electronegativity increases like : PI3, PBr3, PCl3, PF3.
|
c (I) |
c (Br) |
c (Cl) |
c (F) |
|
2,66 |
2,96 |
3,16 |
3,98 |
c (I) < c (Br) < c (Cl) < c (F)
|
102° |
101,5° |
100,3° |
97,8° |
We observe a decrease of these angles. Indeed, the bonding electron pairs are moved near X which have a higher electronegativity than A, and then, confined near X, these pairs exert lower repulsions and the angles decrease.
The second case appears when for same bonding atoms X, we compare the angles between bonds for central atoms A whose electronegativity increases like AsH3, PH3, NH3.
|
c (As) |
c (P) |
c (N) |
|
2,17 |
2,19 |
3,04 |
c (As) < c (P) < c (N)
|
91,58° |
93,83° |
107° |
Addition of the two effects : volume and electronegativity
The two effects seen can partially add or compensate. In molecules like C2H4 and
C2F2H2, the angles between simple bonds are lower than
120°. This is because the volume of the double bonds is higher than the
volume of single bonds. In C2F2H2 this diminution
is higher than in C2H4 because F has an electronegativity higher than H and then the bonding pairs
confined near F exert lower repulsions.
|
118° |
109° |
Non equivalence between axial and equatorial positions in trigonal bipyramidal geometry
We have already seen, that the equatorial and axial positions aren't equivalent in molecules
like PF5 or PCl5. The interaction between bonding electron pairs in equatorial
position is less than in axial position. So there is a decrease of the length for the equatorial bonds and an increase for the axial bonds.
|
Bond |
P-Cléq |
P-Clax |
|
d (nm) |
0,202 |
0,214 |
The non equivalence between axial and equatorial positions is visible when the bonding atoms X are different. For example, in PF3Cl2, Cl has a lower electronegativity than F and the electron pair that provides the bond between P and Cl occupies a higher volume than this between P and F and so, the molecule with Cl in equatorial positions is the stablest.
|
PCl5 |
PF3Cl2 |
Remark : The same effect is observed in the octahedral arrangement. For AX5E molecules like BrF5 (square pyramidal), we observe a small diminution of the angle between bonds Br-Feq and Br-Fax (85° instead of 90°) due to a higher volume occupied by the non-bonding pair and the axial bond is longer that the equatorial ones.
|
Bond |
Br-Feq |
Br-Fax |
|
d (nm) |
0,177 |
0,168 |
Limits of VSEPR method
The VSEPR method often permits the correct prediction for the local arrangement of electron pairs arround an atom when this one is the central atom without ambiguity but for complex molecules it's more difficult to forsee the global geometry. For example it's impossible to forsee that C2H4 is a flat molecule or that in (allenes) the substituants are in perpendicular plane.
Morever, molecules aren't static objects, this is clear in molecules with pyramidal atoms like NH3 or PH3 . It exists some phenomenons more complex too, like the exchange between axial and equatorial positions in trigonal bipyramidal geometry (Berry's pseudo-rotation).
References
R. J Gillespie et R. S Nyholm - Quart. Rev., 1957, 11, 339.
R. J Gillespie - Actualité chimique, 1973, 4, 27.
R. J Gillespie - Molecular geometry, 1972. Van Nostrand Reihold, Londres.
G. Fontaine - Bulletin de l'union des physiciens n° 591 p. 559-568.
J. Sala- Pala - Bulletin de l'union des physiciens n° 648 p. 201-244.
N. N Greenwood and A. Earnshaw - Chemistry of the elements Pergamon Press
1984.
Links
VSEPR Theorie - Caroline Röhr, Universität Freiburg
VSEPR - by M. Lerner, Oregon State University
VSEPR - by Mark Winter, University of Sheffield
VSEPR - by John J. Nash, Purdue University
[HOME PAGE] - [MOLECULAR DATABASE]
For educational purpose. No commercial use.