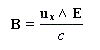
Cours de chimie Organique - G. Dupuis - Lycée Faidherbe de Lille
Chiralité et activité optique
Lumière polarisée
Introduction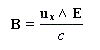
Une lumière est polarisée rectilignement quand E vibre toujours dans un même plan appelé plan de vibration. Le plan perpendiculaire à E dans lequel vibre le champ magnétique B est appelé plan de polarisation.
Dans la lumière naturelle, le vecteur E peut prendre toutes les directions perpendiculaires à la direction de propagation.
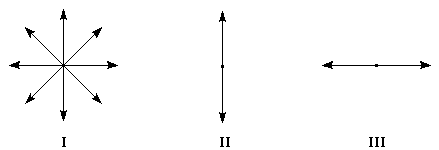
|
Figure |
I |
II |
III |
|
Lumière |
naturelle |
polarisation verticale |
polarisation horizontale |
Loi de Malus
Le physicien français E. Malus découvrit en 1808 le phénomène de polarisation de la lumière en observant, à travers un cristal de tourmaline biréfringent, la réflexion du Soleil couchant sur les fenêtres du palais du Luxembourg.
Plaçons deux polariseurs l'un derrière l'autre, le second est alors appelé analyseur, et envoyons sur le polariseur un faisceau de lumière naturelle :
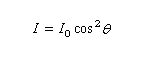
Comment polariser la lumière ?
Plusieurs phénomènes physiques peuvent être mis à profit pour polariser la lumière :
Définitions
L'activité optique est la propriété que possède une structure chirale d'interagir avec un rayonnement électromagnétique . Elle se manifeste par l'existence du pouvoir rotatoire, le phénomène de dispersion optique (DRO), le dichroïsme circulaire (DC) et la polarisation circulaire d'émission.
Le terme chiroptique qualifie les techniques optiques utilisées pour l'étude de la chiralité des molécules. Il s'applique, à la polarimétrie, aux mesures de la dispersion rotatoire optique et du dichroïsme circulaire.
Mise en évidence expérimentale
L'activité optique se manifeste à l'état solide, à l'état liquide ou pour des substances dissoutes. Dans ce qui suit on s'intéresse au dernier cas.
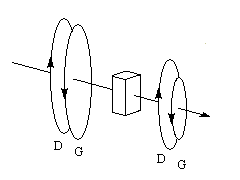
Plaçons successivement : une source de lumière quasi monochromatique S (lampe à vapeur de sodium), un polariseur P, une cuve destinée à recevoir la substance à analyser C, un analyseur A dont l'axe est perpendiculaire au polariseur. L'intensité de la lumière transmise par le dispositif est nulle.

Théorie cinématique de Fresnel du pouvoir rotatoire
L'étude de l'activité optique fait intervenir l'interaction entre une onde électromagnétique et la matière. Une théorie satisfaisante de ce phénomène doit donc être basée sur la
mécanique quantique. Il est cependant possible d'envisager une approche phénoménologique à l'échelle macroscopique. Le modèle ci-dessous est dû au physicien français A. Fresnel.
Dans ce qui suit, l'œil de l'observateur reçoit le rayon lumineux. Une lumière polarisée rectilignement dans un plan vertical est caractérisée par le vecteur champ électrique E.
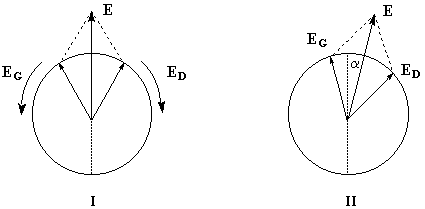
Le vecteur E peut être considéré comme la somme de deux vecteurs EG et ED en phase, de même amplitude et de même fréquence mais tournant en sens inverse.
Dans un milieu inactif (figure I) les champs se déplacent à la même vitesse. A la sortie du milieu, le plan dans lequel vibre E n'a pas changé de direction.
Un milieu actif possède des propriétés physiques dissymétriques pour les champs EG et ED. Cette dissymétrie se traduit, à l'échelle macroscopique, par des indices nG et nD différents. La vitesse de EG est alors différente de celle de ED.
VG = c/nG et VD = c/nD
A la sortie du milieu optiquement actif, on peut montrer que l'un des champs présente un certain déphasage par rapport à l'autre. La lumière est toujours polarisée rectilignement mais le plan de vibration a tourné d'un angle a. La formule de Fresnel relie les grandeurs suivantes :a
: pouvoir rotatoire ou angle de rotation du plan de polarisation (deg) ;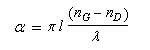
Pouvoir rotatoire, loi de Biot
Cette loi expérimentale, découverte par le physicien français J. B. Biot en 1815, s'applique aux substances optiquement actives dissoutes dans un solvant inactif comme l'eau.
![]()
a
: pouvoir rotatoire ou angle de rotation du plan de polarisation (deg) ;|
a |
> 0 |
< 0 |
|
substance |
dextrogyre (+) |
lévogyre (-) |
Par le passé, le nom de certains composés a été donné en référence explicite au signe de leur pouvoir rotatoire. Ainsi, le D-glucose est également appelé dextrose car ses solutions dévient le plan de polarisation de la lumière vers la droite. Le fructose, isomère cétonique du glucose est appelé lévulose pour la propriété inverse. L'hydrolyse du saccharose (composé dextrogyre) en glucose et fructose s'accompagne d'une inversion du signe du pouvoir rotatoire de la solution ce qui permet d'en effectuer l'étude cinétique par polarimétrie.
Lorsque la solution contient plusieurs substances actives, et que les interactions entre les énantiomères purs sont identiques à celles qui existent dans le mélange, on constate expérimentalement que le pouvoir rotatoire du mélange est la somme des pouvoirs rotatoires des constituants :
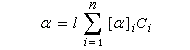
Cette loi est généralement très bien vérifiée, surtout aux faibles concentrations, en l'absence d'effet Horeau.
|
|
|
Les pouvoirs rotatoires spécifiques de deux énantiomères sont opposés. Ainsi, le pouvoir rotatoire d'un mélange racémique est nul par compensation.
Dispersion rotatoire
Lorsqu'on réalise l'expérience de mise en évidence de l'activité optique d'un composé actif entre polariseurs croisés, avec une lumière non monochromatique, on constate qu'il n'est pas possible d'obtenir une extinction complète en tournant l'analyseur. Cela vient du fait que le pouvoir rotatoire spécifique de la substance dépend de la longueur d'onde. Autrement dit, les radiations de différentes longueurs d'ondes dont est composée la lumière
ne tournent pas du même angle lors de la traversée de l'échantillon.
Les courbes représentant les pouvoirs rotatoires spécifiques respectifs de deux énantiomères en fonction de la longueur d'onde peuvent être monotones ou présenter un point d'inflexion pour les courtes longueurs d'ondes. Elles ont alors l'allure suivante :
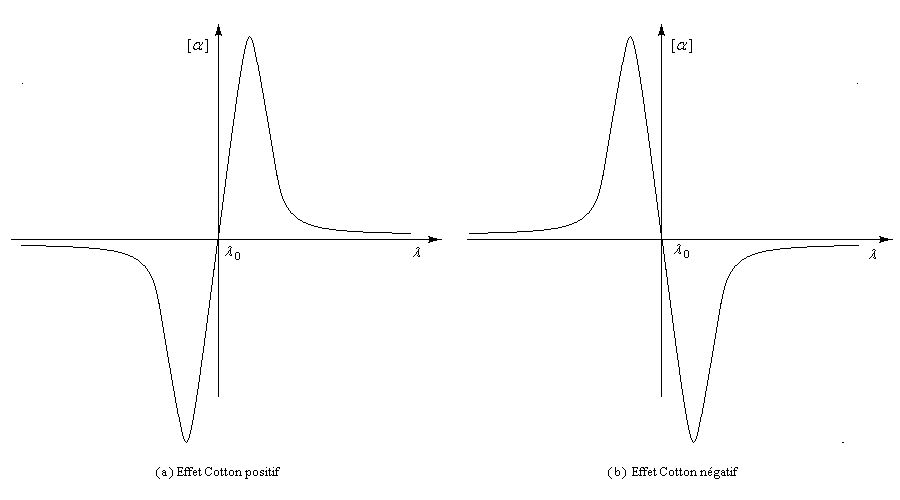
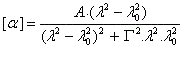
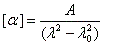
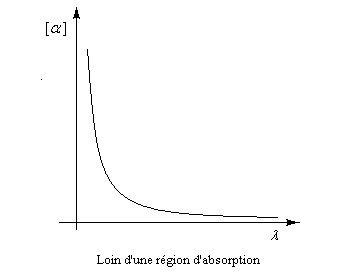
Il n'existe a priori aucune relation évidente entre le signe de l'effet Cotton et la configuration absolue d'une molécule. Cependant l'analyse des courbes de dispersion rotatoire apporte des renseignements précieux sur la structure des molécules. Elle a été appliquée à partir des années 50 par C. Djerassi et son équipe à la résolution de problèmes stéréochimiques. Il est en effet possible de relier le signe de l'effet Cotton avec la stéréochimie lorsqu'il existe des chromophores (comme le groupe carbonyle), se trouvant à proximité d'un élément de chiralité. Grâce à la règle dite des octants, l'étude des spectres de dispersion rotatoire apporte des informations très précieuses sur la stéréochimie de ces composés. Elle permet ainsi de compléter d'un point de vue stéréochimique les résultats concernant la constitution obtenus en spectroscopie UV par application des règles de Woodward et de Woodward-Fieser. Cette méthode a largement contribué à l'élucidation de la structure de nombreuses molécules stéroïdes dans les années 1950 à une époque où les méthodes spectrales étaient encore balbutiantes [32].
Dichroïsme circulaire
Une approche classique simplifiée, consiste à rendre compte du dichroïsme circulaire par l'existence de deux coefficients d'extinction différents eG et eD pour les ondes polarisées circulairement droite et gauche. Après la traversée du milieu, les extrémités des projections des champs ED et EG sur le plan perpendiculaire à la direction de propagation, décrivent des cercles de rayons différents.
Posons :
![]()
Les courbes représentant De en fonction de la longueur d'onde l ont l'allure suivante :
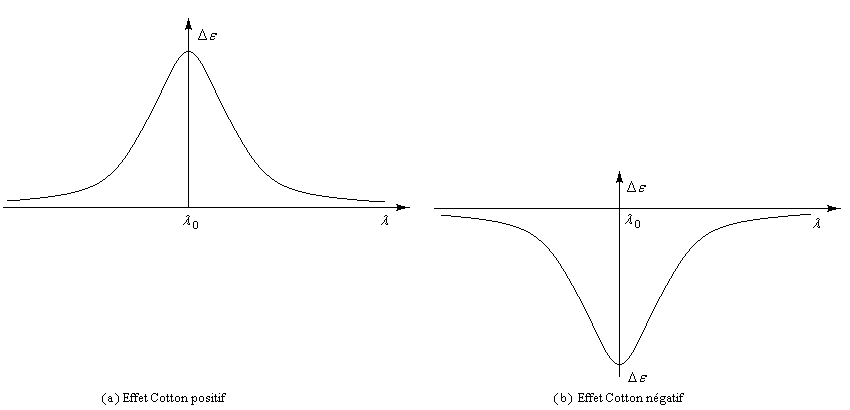
![]()
![]()
La mesure expérmentale de l'ellipticité est un moyen d'accéder à la pureté énantiomérique d'un mélange [24].
Le phénomène de dichroïsme circulaire est particulièrement sensible à la position des atomes dans les molécules. On peut ainsi étudier la dynamique des conformations moléculaires. Une information concernant le repliement secondaire des protéines peut être obtenue rapidement. Chez les protéines, il est possible de distinguer les structures en hélices a, et en feuillets b. Lorsque les protéines comportent des repliements secondaires, une déconvolution en composantes élémentaires du spectre de dichroïsme permet d’estimer grossièrement les proportions de chacun des motifs. Cette technique a été mise à profit très récemment pour l'étude de la structure du prion responsable de L'ESB.
Relation entre chiralité et activité optique
La chiralité est une propriété structurale des molécules dissymétriques. L'activité optique est une manifestation physique, parmi d'autres, de la chiralité. C'est le chimiste français L. Pasteur qui, dans son étude remarquable concernant les acides tartriques a été
le premier à mettre en relation l'activité optique et la chiralité.
L'origine microscopique de l'activité optique provient de la variation du chanp électromagnétique sur l'étendue de la molécule lors de l'interaction lumière-matière (non localité).
Ce lien étroit entre chiralité et activité optique, fait qu'à quelques exceptions près, un composé chiral est optiquement actif et inversement un composé optiquement actif est chiral.
|
|

Configuration absolue et pouvoir rotatoire
La configuration absolue d'une entité moléculaire peut dans certains cas être déterminée directement par l'expérience. La première détermination de ce type a été réalisée par le chimiste hollandais J. M. Bijvoet (Université d'Utrecht) en 1951. En utilisant une technique spéciale de diffraction des rayons X, Bijvoet a pu déterminer la structure spatiale du sel de sodium et de rubidium de l'acide (+)-tartrique [34]. Elle est dessinée à gauche sur le dessin ci-dessous en représentation de Fischer :
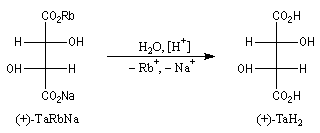
L'expérience montre, par ailleurs, que le traitement acide de ce sel fournit l'acide (+)-tartrique. Puisque cette réaction ne modifie pas la géométrie des atomes de carbone asymétriques de cette molécule, on en déduit que la configuration de l'acide (+)-tartrique est celle qui est indiquée à droite. L'acide (+)-tartrique est donc l'acide (2R, 3R)-dihydroxybutane-1,4-dioïque.
Bien avant l'expérience de Bijvoet, on avait pu montrer, par des réactions de corrélation purement chimiques, que la configuration de l'acide (+)-tartrique était la même que celle du (+)-glycéraldéhyde. Ces composés conduisent en effet tous les deux à l'acide (-)-glycérique au terme de réactions qui ne modifient pas la configuration absolue de l'atome de carbone C2.
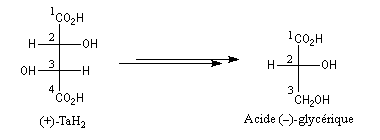
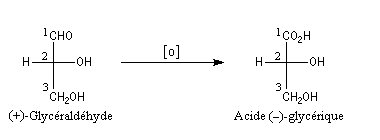
Il n'existe pas de relation simple entre la configuration absolue d'une molécule et le signe du pouvoir rotatoire. Une modification, même minime en apparence de la structure, peut modifier complètement le pouvoir rotatoire.
L'acide lactique dextrogyre est l'acide (S)-2-hydroxypropanoïque pour lequel [a] = 3,3 °.dm-1.g-1.cm3. L'estérification avec le méthanol conduit au (2S)-2-hydroxypropanoate de méthyle, lévogyre pour lequel : [a ] = - 8,2 °.dm-1.g-1.cm3.
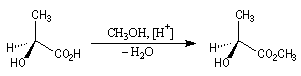
Le pouvoir rotatoire spécifique de certains corps comme l'acide aspartique, change de signe avec la température.
Pureté optique, excès énantiomérique
Considérons une solution constituée d'un mélange d'énantiomères A1 et A2. Faisons l'hypothèse que l'isomère dextrogyre A1 est prépondérant et qu'il existe une certaine quantité de l'énantiomère A2, de sorte que le pouvoir rotatoire a que l'on mesure est inférieur à celui, ao que présenterait une solution de même concentration de l'énantiomère pur A1.
On appelle pureté optique po du mélange, le rapport des pouvoirs rotatoires spécifiques :
![]()
Indépendamment de ce qui précède, désignons respectivement par C1 et C2 les concentrations des énantiomères A1 et A2. L'excès énantiomérique ee est défini par :
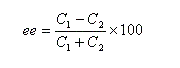
soit :
il y a donc dans ce cas particulier mais fréquemment rencontré égalité entre pureté optique et excès énantiomérique.
Effets non linéaires, effet Horeau
Plusieurs observations expérimentales montrent que la loi d'additivité dont on a parlé plus haut n'est pas toujours vérifiée. C'est le cas par exemple lorsqu'il y a formation de dimères entre les molécules. En 1968, Krow and Hill ont montré que le pouvoir rotatoire spécifique de l'acide 2-éthyl-2-méthylsuccinique possédant une composition en énantiomères de 92.5 % de S et 7.5 % R (ce qui correspond à une excès énantiomérique de 85% ee) varie avec la concentration et change de signe quand la concentration croit.
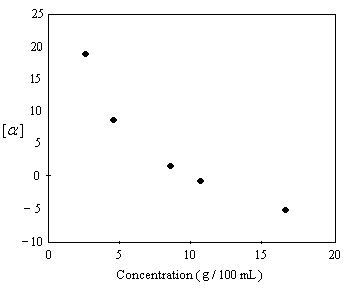
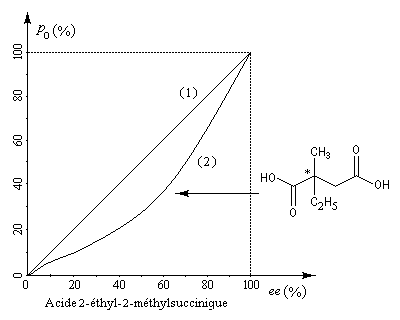
A la suite des travaux de Krow et Hill, le chimiste français Horeau s'est intéressé à la relation entre la pureté optique et l'excès énantiomérique dans le cas de l'acide 2-éthyl-2-méthylsuccinique [30]. La courbe (2) montre que la relation entre ces deux grandeurs n'est pas linéaire. Cet effet, qui s'observe notamment dans les solvants peu polaires, porte le nom d'effet Horeau du nom de son découvreur en 1969 [31].
Bibliographie
Ouvrages théoriques
[1] J. March, Advanced organic chemistry, Wiley Interscience.
[2] F. A. Carey, R. J. Sundberg, Advanced organic chemistry, 3d edition, Plenum Press, 1990.
[3] André Collet, Jeanne Crassous, Jean-Pierre Dutasta, Laure Guy. Molécules chirales : stéréochimie et propriétés. EDP Sciences, CNRS Editions.
[4] Morrison J. D, Mosher H. S. Asymmetric Organic Reactions. Prentice-Hall ; Englewood Cliffs, NJ : 1971.
[5] E. L. Eliel, S. H. Wilen, Stéréochimie des composés organiques, Tec et Doc.
[6] H. Kagan, La stéréochimie organique, PUF, 1975.
[7] J. -L. Pierre, Principes de stéréochimie organique statique, A. Colin, 1971.
[8] P. Laszlo, P. J. Stang, Spectroscopie organique, Hermann 1972.
[9] A. Kirmann, J. Cantacuzène, P. Duhamel - Chimie organique T 1, A. Colin, 1971.
[10] K. Mislow, Introduction to stereochemistry, W. A Benjamin, New York, 1966.
[11] J. Jacques, La molécule et son double, Hachette, 1992.
[12] E. Charney, The Molecular Basis of Optical Activity, Optical Rotatory Dispersion and Circular Dichroïsm, Wiley, New-York, 1979.
[13] Nina Berova, Koji Nakanishi, Robert W. Woody, Circular dichroism : principles and applications. Wiley, New-York
[14] Enantiomers, racemates, and resolutions, Jean Jacques, André Collet, Samuel H Wilen 1981
[15] D. B. Cline, Physical Origin of Homochirality in Life (American Institute of Physics,
New-York, 1996)
[16] P. Drüde : The theory of optics. Dover, New York (U.S.A.) (1959).
Liens
[20] Animation à propos de la polarisation rectiligne (Université de Liège)
[21] Applet Java illustrant la décomposition de Fresnel
[22] A tribute to Carl Djerassi : Reflexions on a Remarkable Scientific Entrepreneur
[23] Do the Terms “% ee” and “% de” Make Sense as Expressions of Stereoisomer Composition or Stereoselectivity ? by Robert E. Gawley
[24] Détermination expérimentale de puretés énantiomériques
[25] Fresnel vu par les chimistes par J. Crassous,
[26] Polarisation de la lumière
Patrick Kohl.
Articles
[30] Krow G, Hill R. K. Chem Commun. 1968 : 430–431.
[31] A. Horeau, Tetrahedron Letters, 1969, 3121-3124.
[32] Moffit W, Woodward R B, Moscowitz A, Klyne W, Djerassi C. Structure and the optical rotatory dispersion of saturated ketones. J. Am. Chem. Soc. 83 ; 4013-18, 1961.
[33] Wynberg, H.; Hekkert, G. L.; Houbiers, J. P. M.; Bosch, H. M. J. Am. Chem. Soc. 1985, 87, 2635–2639.
[34] Peerdeman, A. F., van Bommel, A. J., Bijvoet, J. M. Nature 168, 1951, 271.
Gérard Dupuis - Lycée Faidherbe - LILLE
décembre 2011