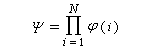
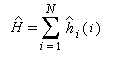
Cours de chimie Organique - G. Dupuis - Lycée Faidherbe de Lille
Les outils du raisonnement en chimie organique
Orbitales moléculaires
Introduction
Les bases de la chimie quantique et l'application à l'étude des molécules sont remarquablement écrite à la référence [35].
Théorie des orbitales moléculaires
L'approximation orbitale est basée sur deux hypothèses :
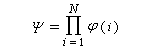
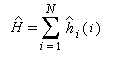
Chaque énergie est solution d'une équation de Schrôdinger relative à un hamiltonien monoélectronique dont ji est une fonction propre.
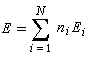
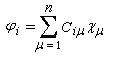
ces orbitales moléculaires ji sont normées ; la condition de normalisation s'écrit :
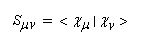
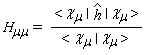
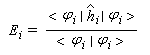
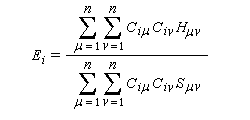
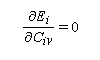
Ei est de la forme u/v. Ce quotient est extremum pour udv - vdu = 0. On a donc :
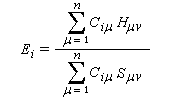
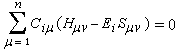
Pour une mise au point sur la théorie des orbitales moléculaires voir : [35].
Méthode de Hückel simple Ces approximations sont résumées, avec les notations usuelles, dans le tableau ci-dessous : Hmm Hmn Hmn Smn a b (atomes liés) 0 dmn L'approximation la plus radicale de la méthode (HMO) consiste à négliger l'intégrale de recouvrement entre les atomes liés. Notons que le recouvrement est pris en compte dans la méthode de Hückel étendue (EHMO) [50]. Il est important de se rappeler que les intégrales a et b sont toutes les deux négatives. Dans le cadre de l'approximation précédente,
le système des équations s'écrit : ce système homogène possède des solutions nulles comme solutions triviales. Il possèdera des solutions autres que nulles à condition que :
Cette approximation de la théorie des orbitales moléculaires a été introduite par le théoricien allemand E. Hückel en 1931. Elle est connue sous le nom de méthode HMO (Hückel Molecular Orbital). La méthode n'est utilisable en toute rigueur que pour les molécules planes car la notion d'orbitale moléculaire de type p ne possède un sens précis que dans ce cas. D'autre part on s'intéresse uniquement au système des électrons p en partant de l'idée que les orbitales s ont une énergie beaucoup plus basse que celle des orbitales p. On admet alors, en première approximation, que les électrons p se déplacent dans un champ moyen créé par les noyaux et les électrons s du squelette non polarisable de la molécule.
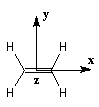
Dans ce qui suit on notera cm les orbitales p des atomes de carbone du squelette, qui sont perpendiculaires au plan de la molécule.
Les approximations de Hückel consistent à poser :
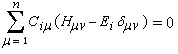
![]()
Les inconnues Ei n'apparaissent donc que dans la diagonale principale du déterminant, ce qui facilite son calcul.
La condition de normalisation se réduit à :
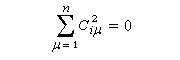
Le système d'équations relatif à une orbitale moléculaire ji s'écrit :
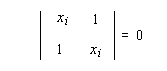
Le tableau suivant regroupe les valeurs numériques des coefficients :
|
Energie |
Ci1 |
Ci2 |
|
E1 = a + b |
0,707 |
0,707 |
|
E2 = a - b |
0,707 |
-0,707 |
Les orbitales moléculaires p et p* ont respectivement pour expression :
Le schéma ci-dessous représente ces om ainsi que leur énergie.
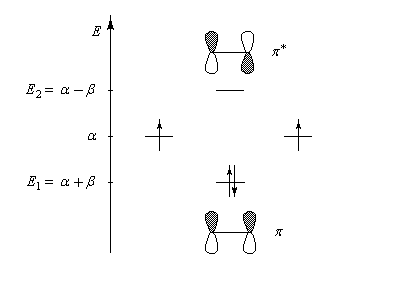
L'écart énergétique entre le niveau antiliant et le niveau de départ est le même que l'écart entre celui-ci et le niveau liant. Ce résultat vient du fait que le recouvrement est négligé.
Dans la méthode HMO, les intégrales de recouvrement entre atomes différents sont toutes nulles. Pour caractériser la population de recouvrement, C. A. Coulson a proposé d'introduire la notion d'indice de liaison p :
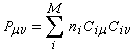
ni est le nombre d'électrons décrit par l'orbitale ji. La somme est étendue aux M orbitales occupées. Dans le cas de l'éthène, on obtient :
cela est bien en accord avec un ordre de liaison total égal à deux pour la molécule.
La présence d'hétéroatomes, dans le système conjugué est prise en compte grâce à des modèles semi-empiriques.
|
|
Nombre d'électrons |
Intégrale coulombienne |
Intégrale de résonance |
|
azote |
2 |
a N = a + 1,5 b |
b CN = 0,8 b |
|
oxygène |
2 |
a O = a + 2 b |
b CO = 0,8 b |
|
chlore |
2 |
a Cl = a + 2 b |
b CCl = 0,4 b |
|
CH3 (modèle hétéroatomique) |
2 |
a Me = a + 2 b |
b CMe = 0,7 b |
Formules de Coulson Les valeurs propres xi, sont données par :
Les énergies Ei ont donc pour expression :
Les valeurs de l'énergie sont donc tojours comprises comprises entre a + 2 b et a - 2 b. Puisque le nombre de niveaux d'énergie est égal au nombre d'atomes n du polyène, il en résulte que les niveaux se ressèrent quand n augmente. Il en va de même en ce qui concerne l'écart entre la plus haute om occupée (HO) et la plus basse om vacante (BV).
Les résultats précédents peuvent être généralisés aux polyènes linéaires.
Soit n, le nombre d'atomes de carbone du polyène. La formule générale est CnH2n-2.
Les coefficients Cim des orbitales atomiques cm de l'orbitale moléculaire ji sont donnés par (i varie de 1 à n) :
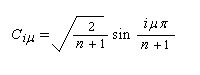
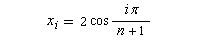
Les xi sont liées à l'énergie par associée à chaque orbitale moléculaire par :
(on notera que la valeur xi = 0
n'existe pas : il n'y a pas d'om non liante).
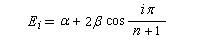
On onterprète par ce modèle simple, le caractère conducteur des poyènes à longue chaîne tel que le polyacétylène.
Pour une mise au point sur la théorie de Hückel voir, par exemple [22] (Chap. 7) et [35] p. 71 et suiv. Méthode de Hückel étendue (EHMO) K est un paramètre ajustable qui permet de mettre en conformité valeurs expérimentales et valeurs calculées. En général, la valeur prise est : K = 1,75. Les orbitales moléculaires p et p* ont respectivement pour expression : Le schéma ci-dessous représente ces orbitales moléculaires ainsi que leur énergie relative.
Cette méthode a été proposée par R. Hoffmann. Elle est basée sur les approximations suivantes :
![]()
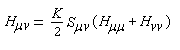
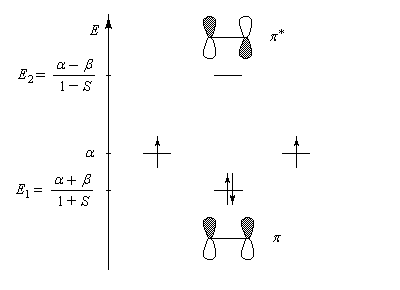
Il est important de noter que l'écart énergétique entre le niveau antiliant et le niveau de départ est plus grand que l'écart entre celui-ci et le niveau liant. La méthode EHMO donne ainsi un résultat plus fidèle à la réalité que la méthode HMO dans laquelle le recouvrement n'est pas pris en considération.
Perturbations
Nous nous limiterons aux principaux résultats dans les cas les plus simples. Les calculs sont développées aux références : [21] (introduction : voir Chap. 4) et [22] (p. 117 et suiv. A un niveau plus avancé.)
Interaction entre deux om dégénénérées
Interactions entre deux om non dégénérées
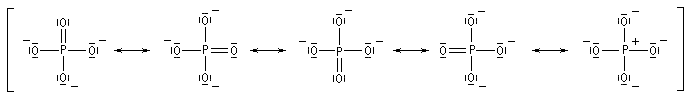
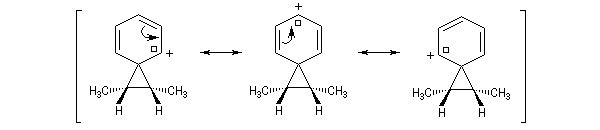
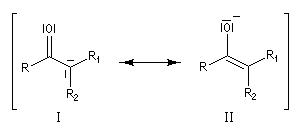
Les différentes formes mésomères ne possèdent pas la même importance dans la description de la molécule réelle. On peut classer ces formes selon leur poids statistique de la manière suivante. Les formes qui contribuent le plus à la structure réelle sont celles qui :
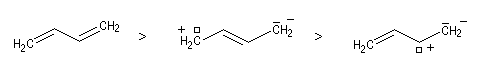
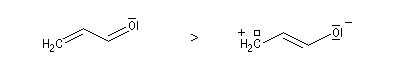
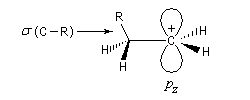
Approximation des orbitales frontières Exemple de la molécule d'éthène
Dans ce qui suit, on désignera par HO, la plus haute orbitale moléculaire occupée (en énergie) de l'un des réactifs et par BV la plus basse orbitale moléculaire vacante de l'autre. En anglais, ces orbitales sont notées respectivement HOMO (highest occupied molecular orbital) et LUMO (lowest unoccupied molecular orbital).
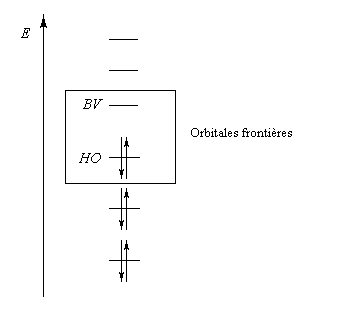
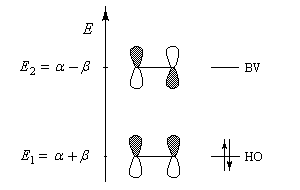
Les orbitales frontières de la molécule d'éthène dans le cadre de la méthode de Hückel simple :
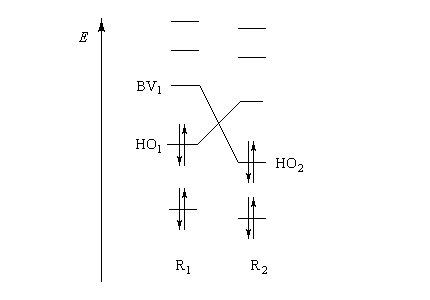
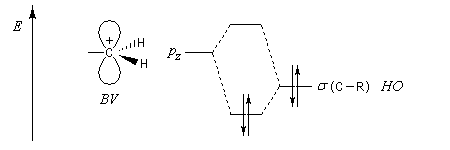
Pourquoi les orbitales frontières ont-elles un tel intérêt ? On peut le comprendre en examinant le diagramme énergétique ci-dessous.
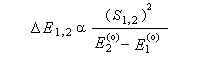
Lorsque les molécules ne sont pas identiques les énergies de leurs orbitales frontières sont différentes.
L'interaction dominante est celle qui implique les OF dont l'énergie est la plus proche
Dans l'exemple ci-dessous, il s'agit de l'interaction entre HO1 et BV2 schématisée en trait plein sur la figure.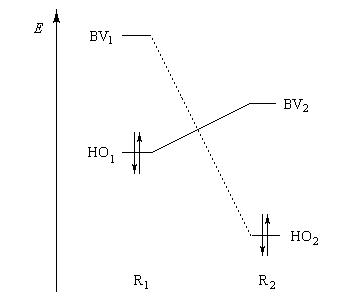
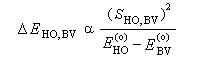
Pour une mise au point sur la théorie des orbitales frontières voir : [21] (Chap. 5 : introduction ; application aux cycloadditions) et [35] (niveau plus avancé) ainsi que [24].
Il existe une approche complémentaire fondée sur les théories de fonctionnelles de densité (DFT) : les fonctions de Fukui.
Réactions péricycliques
Une réaction péricyclique est un processus concerté (en anglais : concerted) au cours duquel la réorganisation des liaisons passe par état de transition cyclique.
Voici des exemples de telles réactions :
Caractère suprafacial et antarafacial
Les termes suprafacial et antarafacial précisent la manière dont se créent ou se brisent deux liaisons au cours d'une réaction impliquant un fragment moléculaire. Les éléments stéréochimiques de référence sont les "faces" du système orbitalaire.
Commençons par le cas simple ou l'élément est constitué d'une seule orbitale p (cet élément, noté w, peut correspondre à un carbocation ou à un carbanion). Les "faces" de référence sont les deux côtés du plan P.
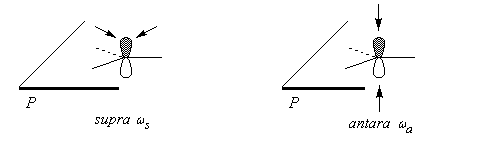
Considérons à présent un système p constitué de deux électrons (ce fait est noté par le chiffre 2 en exposant).
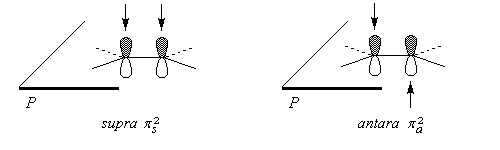
Pour un polyène conjugué C1 - Cp comportant p atomes de carbone et donc aussi p électrons p, on aura de même le schéma suivant :
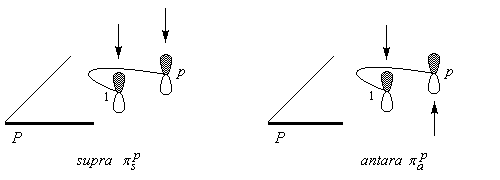
Le caractère suprafacial ou antarafacial s'étend aux réactions impliquant des liaisons s
Pour des compléments sur ces questions voir : [24] et [30]
Cycloadditions
Soient deux polyènes conjugués C1 - Cp et C1' - Cq possédant respectivement p et q atomes de carbone. Une cycloaddition [p + q] conduit à un adduit cyclique résultant de la formation des liaisons C1 - C1' et Cp - Cq des polyènes précédents.
La géométrie d'une cycloaddition peut, selon les cas, avoir lieu de façon supra-supra ou bien supra-antara.
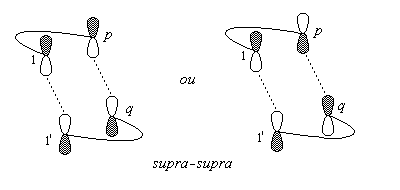
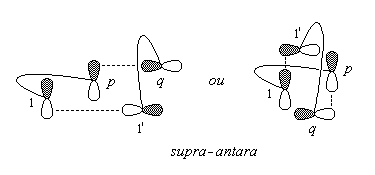
L'expérience montre que la cyclodimérisation de l'éthène est impossible par voie thermique.
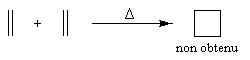
Afin de rationaliser ce résultat, plaçons côte à côte les orbitales frontières des molécules A et B susceptibles d'interagir entre-elles.
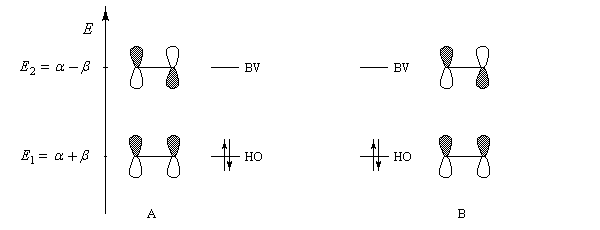
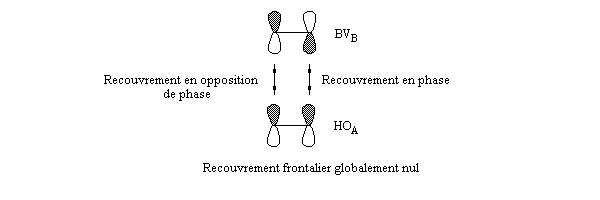
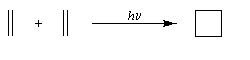
Par irradiation, un des électrons de la molécule A peut être promu à un niveau d'énergie supérieur (HO*).
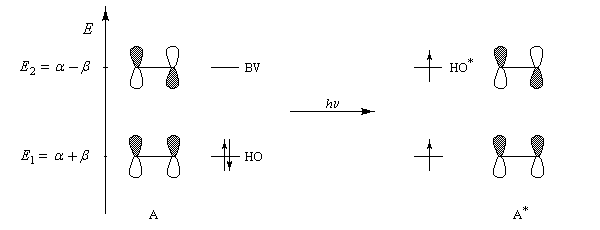
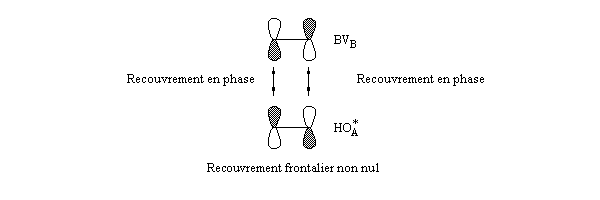
L'interaction entre HO* d'une molécule (A) et BV de l'autre molécule (B) devient possible.
Autre exemple étudié dans le chapitre sur les systèmes conjugués : la cycloaddition entre l'éthylène et le buta-1,3-diène ou réaction de Diels-Alder est permise par voie thermique.
Compléments voir : [21] (OF, cycloadditions), [22] (chap 7. Méthode de Hückel et 8. réactivité) et [41] (plus spécialement consacré aux règles de WH.)Complément : Equation de Klopman-Salem
Désignons par r et s les atomes qui interagissent lors de l'approche des réactifs R et S avec formation d'un adduit RS. La méthode des perturbations appliquée au système au début de la réaction permet de calculer la différence d'énergie entre RS et R + S. Elle se présente sous la forme de la somme de trois termes :
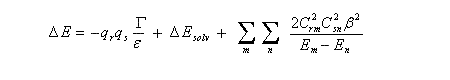
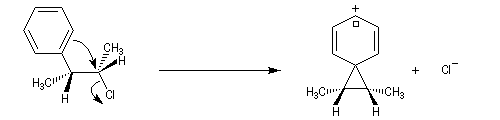
Hyperconjugaison
L'hyperconjugaison consiste en l'interaction entre un niveau électronique occupé et un niveau innocupé de plus haute énergie.
Exemples :
Examinons à titre d'exemple l'interaction entre des électrons d'une liaison s (C-H) et une orbitale p vacante de plus haute énergie. En termes d'orbitales moléculaires, le phénomène peut être décrit par le diagramme suivant.
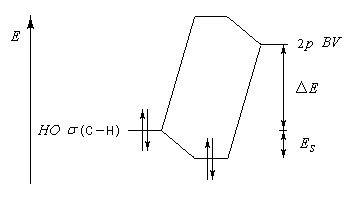
La méthode des perturbations permet de montrer que l'énergie de stabilisation Es est proportionnelle à l'intégrale de recouvrement S et inversement proportionnelle à l'écart d'énergie DE entre les niveaux impliqués. L'énergie globale du système est donc abaissée d'autant plus que le recouvrement est grand et la différence d'énergie entre les niveaux impliqués est plus petite.
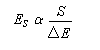
On notera qu'il n'existe pas de différence fondamentale du point de vue énergétique entre conjugaison et hyperconjugaison. Pour un résumé assez détaillé sur cette question voir : [27]
Plusieurs phénomènes s'interprètent en termes d'hyperconjugaison :
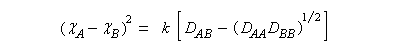
|
H : 2,1 |
- |
- |
- |
- |
- |
- |
|
Li : 0,98 |
Be : 1,57 |
B : 2,04 |
C : 2,55 |
N : 3,04 |
O : 3,44 |
F : 3,98 |
|
Na : 0,93 |
Mg : 1,31 |
Al : 1,61 |
Si : 1,90 |
P : 2,19 |
S : 2,58 |
Cl : 3,16 |
|
K : 0,82 |
Ca : 1,00 |
Ga : 2,01 |
Ge : 2,01 |
As : 2,18 |
Se : 2,55 |
Br : 2,96 |
|
Rb : 0,82 |
Sr : 0,95 |
In : 1,78 |
Sn : 1,96 |
Sb : 2,05 |
- |
I : 2,66 |
Il est commode d'étendre la notion d'électronégativité à celle de groupes d'atomes.
|
Groupe |
H |
CH3 |
C2H5 |
NH2 |
CCl3 |
Ph |
CN |
OH |
NO2 |
|
Electronégativité (Pauling) |
2,1 |
2,3 |
2,3 |
2,8 |
3,0 |
3,0 |
3,3 |
3,4 |
3,4 |
|
|
tétragonal |
trigonal |
digonal |
|
Electronégativité (Pauling) |
2,48 |
2,75 |
3,30 |
Une notion un peu différente, l'électronégativité absolue est une grandeur relative à une entité (atome, molécule, ion) qui caractérise cette espèce dans son ensemble.
Moment dipolaire
Le moment dipolaire m d'un composé est une grandeur physique qui peut être mesuré expérimentalement à partir de la permittivité relative de la substance er , et de la densité. Le moment dipolaire m trouve son origine dans l'existence de liaisons partiellement polarisées dans la molécule. Dans la molécule de chlorométhane
représentée ci-dessous, la polarisation de la liaison C-Cl s'interprète par la différence d'électronégativité entre les atomes C et Cl. Les liaisons C-H, ne sont pratiquement pas polarisées. La liaison C-Cl se comporte comme un petit dipôle
et il est commode de considérer que les atomes C et Cl ont acquis respectivement une charge q = d e et -q = -d e. On représente en général les charges partielles en unité atomique sur les atomes constituant la liaison : d + et d - respectivement. Conformément aux conventions
le moment dipolaire est représenté par un vecteur orienté de la charge négative vers la charge positive.
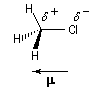
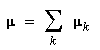
Moments dipolaires de quelques liaisons simples (D)
|
Liaison |
C-H |
Cl-C |
I-C |
N-C |
O-C |
F-H |
I-H |
|
m (D) |
0,4 |
1,46 |
1,19 |
0,22 |
0,74 |
1,82 |
0,44 |
|
Composé |
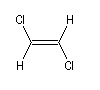 |
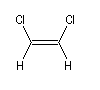 |
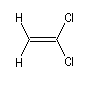 |
|
m (D) |
0 |
1,3 |
1,9 |
Polarisabilité
On appelle polarisabilité la propriété physique associée à la création dans une molécule, d'un moment dipolaire induit mi sous l'action du champ extérieur. La polarisabilité est un phénomène dynamique. Le moment dipolaire
induit s'annule lorsque la cause qui lui a donné naissance a disparu.
Désignons par E*, le champ ressenti par la molécule dans le milieu où elle se trouve (champ électrique augmenté du champ local de Lorentz [17]).
|
Composé |
C-Cl |
C-Br |
C-I |
|
Longueur C-X (pm) |
178 |
193 |
214 |
|
Moment dipolaire m (D) |
1,94 |
1,79 |
1,64 |
|
Polarisabilité relative |
1 |
1,4 |
2,2 |
On notera qu'une molécule est d'autant plus polarisable qu'elle possède une dureté plus faible.
Electronégativité et dureté
|
Composé |
CH3-F |
CH3-Cl |
CH3-Br |
CH3-I |
|
c / eV |
3,2 |
3,8 |
4,8 |
4,9 |
|
h / eV |
9,4 |
7,5 |
5,8 |
4,7 |
Effet inductif
La polarisation d'une liaison est due à la différence d'électronégativité des atomes liés. Elle se caractérise notamment par l'existence d'un dipôle permanent. Ce dipôle peut induire à son tour une polarisation dans une liaison adjacente polarisable.
La transmission de la polarisation à travers des liaisons s par le mécanisme précédent s'appelle "effet inductif".
Les effets inductifs peuvent être classés en deux catégories selon la valeur de leur électronégativité c par rapport à celle de l'atome de carbone (2,5) :
|
|
+ I faibles |
-I forts |
-I faibles |
|
-Na, -Li, -MgR |
alkyle |
-NO2, -CN, -NH3+, -CF3, -N+R3 -CO2H, -CO2R, |
-F, -Cl , -Br , -I, phényle, -OH, -OCH3 |
Effet mésomère
Lorsqu'on examine la valeur des moments dipolaires descomposés ci-dessous, on constate que le composé aromatique nitré possède un moment dipolaire plus grand que le dérivé saturé correspondant tandis que pour les dérivés fluorés c'est l'inverse.
|
Composé |
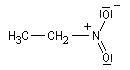 |
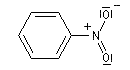 |
|
m (D) |
3,7 |
4,2 |
|
Composé |
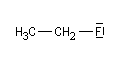 |
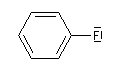 |
|
m (D) |
1,9 |
1,6 |
Ces résultats ne peuvent s'expliquer en considérant seulement les effets inductifs.
Le fluor donne des électrons au cycle. Il s'agit d'un effet donneur.
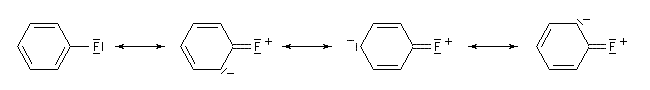
Le groupe nitro accepte des électrons de la partdu cycle. Il s'agit d'un effet attracteur.

Dans le cas de la molécule de nitrobenzène, l’effet inductif et l’effet mésomère vont dans le même sens, la molécule a un moment dipolaire plus grand que celle de nitroéthane. Dans le cas de la molécule de fluorobenzène, l’effet mésomère et l’effet inductif sont antagonistes. La molécule a un moment dipolaire plus petit que celui de la molécule de fluoroéthane.
D'une façon générale, lorsque l'effet mésomère et l'effet inductif sont antagoniste, l'effet mésomère l'emporte sur l'effet inductif.Les types fondamentaux de réaction
Définitions
Lorsque deux entités réagissent, il est commode de distinguer le substrat (étymologiquement : sur lequel se déroule le processus) et le réactif. Le substrat est la molécule organique qui "subit l'attaque" du réactif. Lorsque l'une des entités est inorganique, c'est par convention le réactif. Naturellement, il existe une certaine ambiguité lorsque les deux partenaires sont organiques et l'on raisonne alors par analogie. La conversion d'un substrat en un produit particulier indépendamment de la nature des réactifs mis en jeu est une transformation.
La distinction entre substrat et réactif doit être maniée avec précautions mais elle a une certaine importance pour le classement des réactions et de leurs mécanismes. En effet celles-ci sont nommées selon deux critères :
|
Réactif |
électrophile |
nucléophile |
|
aspect thermodynamique |
||
|
aspect cinétique |
réactivité rapide vis à vis des zones de faible densité électronique |
réactivité rapide vis à vis des zones de forte densité électronique |
Remarque : le terme réactant (en anglais : "reactant") désigne un corps qui est consommé au cours d'une réaction chimique.
Classement
La terminologie du classement des réaction est due à Ingold. On distingue neuf types fondamentaux.
|
Additions |
Substitutions |
Eliminations |
|
électrophile AE |
électrophile SE |
électrophile EE |
Exemples : réaction de substitution nucléophile ;

autres exemples :
Intermédiaires réactionnels
Introduction
Les carbocations sont des ions positifs du carbone il existe deux familles :
Les carbocations peuvent être synthétisés à partir de dérivés halogénés en milieu superacide.
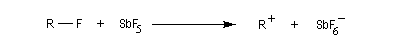
Les carbocations interviennent généralement comme intermédiaires réactionnels. Ce sont des espèces fugaces et leur durée de vie très courte nécessite l'utilisation de technique spéciales d'étude. Parmi celles-ci la spectroscopie de RMN en milieu superacide a été développée par le chimiste américain d'origine hongroise G. Olah. Ses travaux sur la chimie des carbocations ont permis de développer plusieurs concepts nouveaux comme ceux d'ions non classiques et d'atome de carbone hypercoordiné. Ils ont été couronnés par l'attribution du prix Nobel de chimie en 1994. Quelques carbocations ont une durée de vie suffisante pour pouvoir être observés et conservés en solution à la température ambiante [69].
Pour une mise au point complète à un niveau avancé : [37]
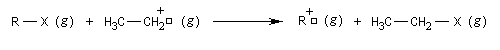
On constate l'ordre de stabilité suivant :
|
Carbocation |
DrG0 (kJ.mol-1) |
|
CH3CH2+ |
0 |
|
CH3CH2CH2+ |
-25 |
|
(CH3)2CH+ |
-92 |
|
(CH3)3C+ |
-167 |
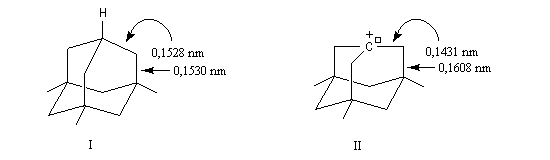
D'une façon très générale, on observe l'ordre de stabilité suivant :
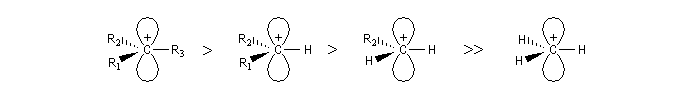
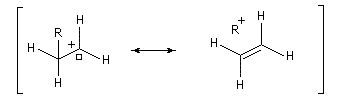
Lorsqu'on passe du dérivé de l'adamentane (I) au cation (II), l'hyperconjugaison se manifeste par un raccourcissement de la liaison C(+) - C et un allongement de la liaison C - C adjacente.
Les carbocations allyliques sont stabilisés par résonance.
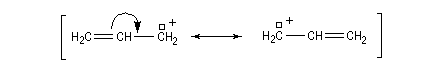
On interprète de la même façon la stabilité des carbocations benzyliques.
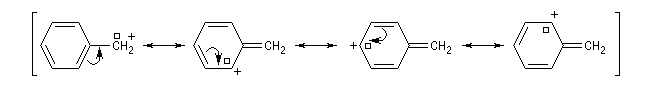
Certains cations doivent leur stabilité relative à leur caractère aromatique. C'est le cas du cation cyclopropénium.
Les ions acylium sont stabilisés par la présence d'un hétéoatome adjacent.
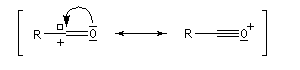
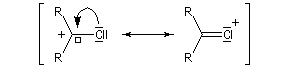
Les ions halonium sont des intermédiaires très réactifs. Du fait de la plus petite taille de l'atome de chlore par rapport à l'atome de brome, les ions chloronium sont en équilibre avec le carbocation ouvert.
Les complexes s encore appelés intermédiaires de Wheland sont des carbocations stabilisés grâce à la conjugaison du sycle aromatique.
Intervention des carbocations dans les mécanismes Les carbocations interviennent dans de nombreux mécanismes :
Transposition de Wagner-Meerwein H. Meerwein montra que la vitesse de la réaction augmente avec la constante diélectrique du solvant et aussi en présence d'acides de Lewis comme AlCl3 ou SbCl5. Le mécanisme de la réaction fait intervenir un carbocation qui subit une réaction de transposition. En fait, une analyse fine de la stéréochimie des produits obtenus lors de la transposition de Wagner-Meerwein, montre que la situation est, plus compliquée. On peut rationaliser les résultats expérimentaux en faisant intervenir deux carbocations non classiques. Chaque fois que des carbocations sont générés dans une réaction, on observe ce type de transposition. Exemples :
Application : préparation de l'adamentane L'adamentane est le tricyclo [3,3,1,1] décane. A la température ordinaire, ce composé se présente comme un solide cristallin de couleur blanche, de point de fusion élevé (> 210 °C). Du point de vue structural, la molécule peut être regardée comme résultant de la fusion de quatre cycles de type cyclohexane en conformation chaise. Les angles entre toutes les liaisons sont ceux qu'on observe dans un tétraèdre régulier d'où l'absence de contrainte interne dans la molécule. La synthèse de Paul von R. Schleyer prend comme point de départ le produit d'hydrogénation catalytique du dicyclopentadiène lui même obtenu par addition de Diels-Alder du cyclopentadiène sur lui même.
A l'origine, cette transposition a été mise en évidence par Wagner. Il s'agissait de la réaction permettant de passer du chlorhydrate de camphène (I) au chlorure de bornyle (II).
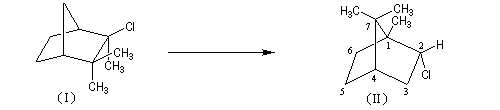
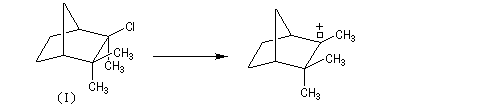
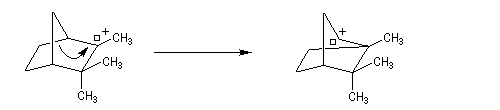
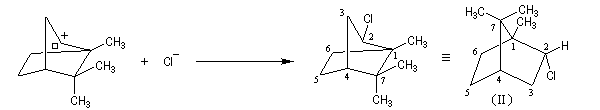
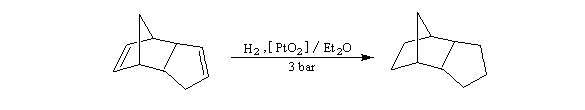
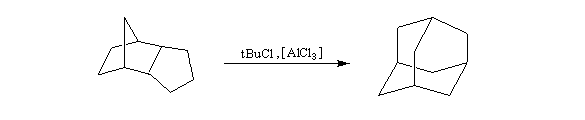
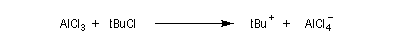
Ce carbocation réagit avec l'hydrocarbure pour fournir un nouveau carbocation par arrachage d'un atome d'hydrogène.
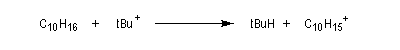
Participation d'un groupement voisin
On s'intéresse aux vitesses d'acétolyse des composés suivants.
|
Composé |
|
|
|
|
Vitesse relative |
1 |
104 |
1011 |
Des deux stéréoisomères, celui qui réagit le plus rapidement est le troisième. Par ailleurs, dans le produit obtenu, on constate que le nucléophile se place au même endroit que le nucléofuge. Il y a rétention de la configuration.
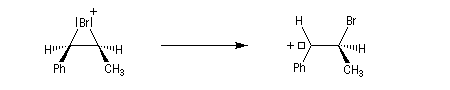
On interprète ces résultats par la formation d'un intermédiaire ponté non classique. Lors de la formation de l'intermédiaire, la double liaison assiste le départ du nucléofuge. On dit qu'il y a eu assistance anchimère du grec ankura : ancre (en anglais : anchimeric assistance ou neighboring group participation).
La réaction du carbocation avec le nucléophile a lieu de façon préférentielle du côté opposé au pont ce qui explique la rétention de configuration observée.
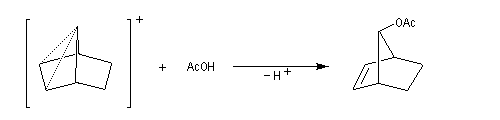
Un autre exemple intéressant concerne la réaction de composés comme le 3-phényl-2-chlorobutane dans lesquels un groupe phényle est situé en b de l'halogène. L'acétolyse du composé de configuration absolue (2S, 3S) conduit à un mélange racémique. On interprète la perte de la chiralité par la formation d'un intermédiaire possédant un plan de symétrie.
Le groupe phényle assiste le départ du nucléofuge. L'intermédiaire obtenu est un cation phénonium dans lequel la charge positive est délocalisée. Il s'agit d'un autre exemple d'assistance anchimère.
On notera l'analogie entre les cations phénonium et les intermédiaires de Wheland rencontrés dans les réactions de substitutions électrophiles aromatiques.
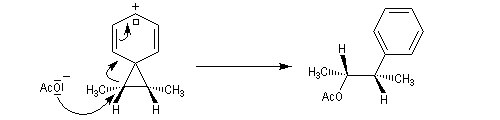
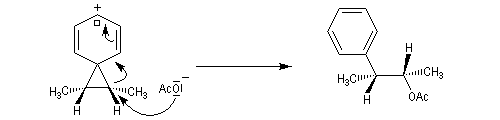
Carbocations non classiques
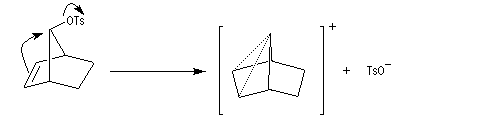
L'étude de la solvolyse des benzènesulfonates d'exo-norbornyle (I) et d'endo-norbornyle (II) a été faite par le chimiste d'origine canadienne Saul Winstein (UCLA) à partir de 1949. Les résultats expérimentaux sont les suivants [71] :
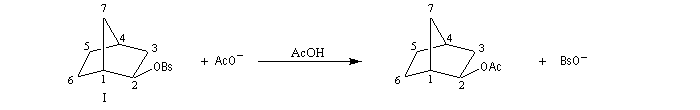
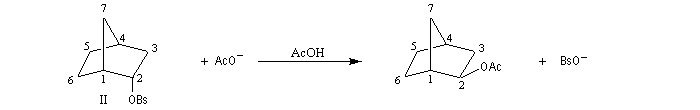
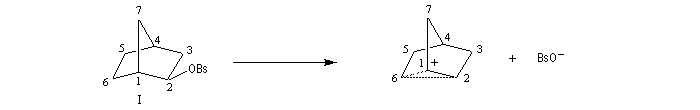
On obtient ainsi un ion "non classique" pour lequel la charge positive est délocalisée sur les atomes de carbone 1, 2, 6. Cet ion possède un plan de symétrie passant par les atomes de carbone C4, C5, C6. Il est donc achiral.
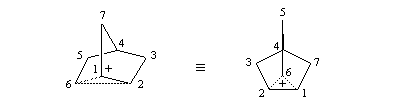
En revanche, l'ionisation du composé endo pour donner l'ion non classique n'est pas assistée. Elle est donc moins rapide. Pour plus de détails on pourra consulter [21].
Le cation norbornyle peut être préparé en milieu superacide et son étude par spectroscopie de RMN a été effectuée.

Aux températures inférieures à -158 °C, le spectre RMN a l'allure suivante.
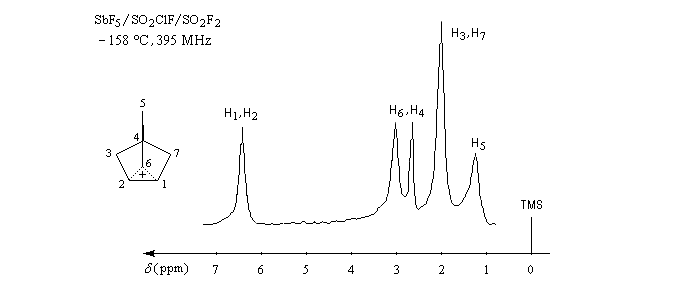
|
Déplacement chimique (ppm) |
Intensité |
Attribution |
|
6,75 |
2 H |
C1, C2 |
|
3,17 |
2 H |
C6 |
|
2,82 |
1 H |
C4 |
|
2,13 |
4 H |
C3 , C7 |
|
1,37 |
2 H |
C5 |
Interprétation de Brown, équilibre entre deux carbocations classiques.
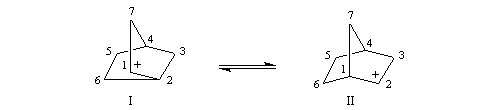
Une synthèse du longifolène due à W. S. Johnson met en jeu un carbocation non classique.
Cette étape est analogue à la réaction de Lucas.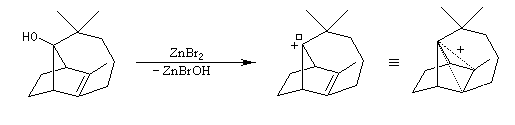
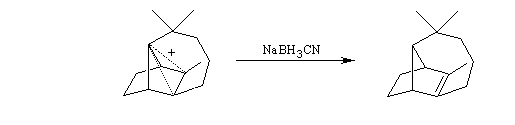
Introduction
On prépare ainsi beacoup d'organolithiens et en particulier le butyllithium. Composés organosodiques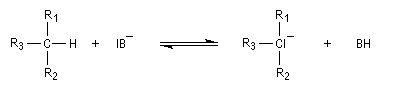
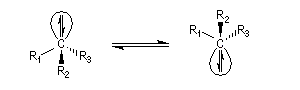
![]()
Les dérivés alkylés les plus simples sont des composés extrêmement réactifs. Ils réagissent sur l'eau avec explosion en donnant un dégagement de dihydrogène. Les termes les plus simples ne sont guère utilisés en synthèse en raison d'une trop grande réactivité basique et nucléophile. Ils réagissent par exemple rapidement sur le substrat qui a servi à les préparer et on observe des réactions de substitution (réaction de Wurtz) et d'élimination.
![]()
Les organosodiques et les organopotassiques attaquent rapidement les éthers comme l'éthoxyéthane en provoquant des réactions d'élimination et la plupart du temps, on les prépare en utilisant un hydrocarbure comme solvant.
A côté des organosodiques proprement dits, les composés dans lesquels la charge négative est stabilisée par délocalisation peuvent être obtenus assez facilement par métallation de la liaison C-H de l'hydrocarbure correspondant avec une base suffisamment forte. Ce sont des sels de sodium dont l'anion est le carbanion formé à partir de l'hydrocarbure.
Un hydrocarbure comme le fluorène (pKa = 23) est suffisamment acide pour pouvoir être déprotoné par l'ion hydroxyde dans le DMSO. On obtient alors un sel de sodium dans lequel l'anion est le carbanion fluorényle.
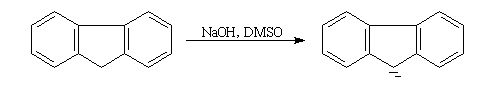
|
|
Un mélange d'hydroxyde de sodium en perles et de fluorène sont ajoutés à une petite quantité de DMSO bien sec. Le mélange est agité à la température ambiante. Au bout d'une quinzaine de minutes, on obtient une solution de couleur rouge qui contient l'anion fluorényle. Cet ion est stabilisé par résonance (le cycle central possède un caractère aromatique). La conjugaison est suffisamment étendue pour qu'il absorbe dans la partie visible du spectre. |
Une autre classe d'organosodiques est constituée par les composés d'addition dans lesquels un substrat organique accepte des électrons de la part d'un métal alcalin. Dans cette catégorie, on trouve les radicaux-anions :
Carbanions stabilisés Un type particulier de carbanion est constitué par les ylures.
Parmi les carbanions stabilisés par un groupe fonctionnel les plus importants sont les énolates :
Les radicaux libres
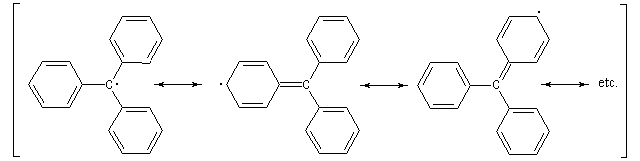
Un radical est une espèce comportant un ou plusieurs électrons non appariés. Le premier radical organique a été mis en évidence par Moses Gomberg en 1900. Il s'agit du radical triphénylméthyle. Le schéma réactionnel utilisé par Gomberg est le suivant :
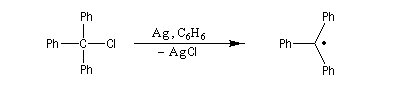
Un moyen classique d'obtention de radicaux consiste en la rupture homolytique de liaisons. Celle des azoalcanes est favorisée du fait de la formation de diazote très stable.
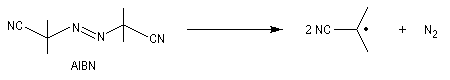
Le tableau ci-dessous donne l'énergie de dissociation de liaisons R-H pour la formation de radicaux alkyles.
|
Radical |
Do (kJ.mol-1) |
|
CH3° |
435 |
|
CH3CH2° |
410 |
|
(CH3)2CH° |
397 |
|
(CH3)3C° |
385 |
Une technique d'étude consiste à les piéger par un réactif (spin trap)afin de former un radical plus stable qui peut être ensuite étudié par résonance paramagnétique électronique (RPE).
Exemple : la 5,5-diméthylpyrroline N-oxyde (ou DMPO) est l’exemple le plus répandu de ce type de "sonde" utilisable en RPE.
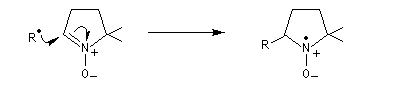
Les radicaux alkyles sont d'autant plus stables que l'atome de carbone est substitué par un plus grand nombre de groupes alkyles.

Comme pour les carbocations, cette stabilisation peut être rationalisée par l'hyperconjugaison résultant du recouvrement d'une orbitale atomique 2pz et d'une orbitale moléculaire s (C-H) du substituant. Certains radicaux comme le radical triphénylméthyle sont qualifiés de non réactifs car ils peuvent être conservés assez longtemps même à la température ordinaire.
Le dioxygène O2 dans son état fondamental triplet est un diradical.
Les réactions chimiques dans lesquelles interviennent des radicaux sont très nombreuses. Citons quelques exemples :
Oxygène singulet
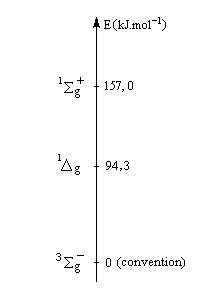
L'état fondamental de la molécule d'oxygène est un état triplet 3Sg. Les deux premiers états excités sont deux états singulets d'énergies respectives 94,3 et 157,0 kJ.mol-1 (schéma de gauche). L'oxygène singulet 1Dg peut être préparé
par irradiation de O2 (3Sg) en présence d'un photosensibilisateur [12].
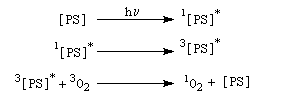
Cinétique chimique
Théorie des collisions
L'énergie d'activation Ea représente la différence entre l'énergie des réactif et celle d'une association d'atomes constituant le complexe activé. Elle correspond donc à l'énergie que doivent acquérir les molécules pour réagir. La détermination de la constante de vitesse de la réaction en fonction de l'énergie d'activation est l'un des objectif de la théorie des collisions [38].
|
|
|
|
|
|
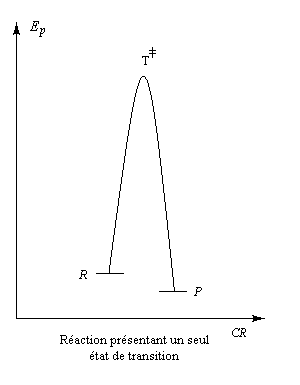
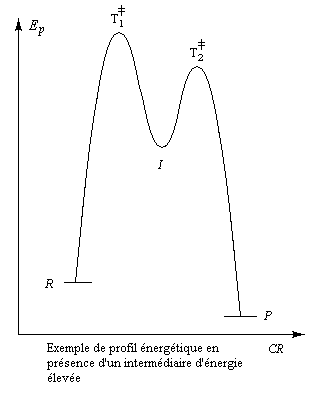
L'enthalpie libre molaire de référence de l'état de transition est la somme de l'enthalpie libre molaire des réactifs et de l'enthalpie libre d'activation de référence (le symbole typographique utilisé en exposant se lit "double dague".) Pour une mise au point sur ces questions et notamment sur les différentes façons d'aborder les problèmes selon l'échelle à laquelle on se place, voir : [56] et [57].
![]()
La constante de vitesse k de la réaction est liée à l'enthalpie libre d'activation de référence par l'équation d'Eyring. Elle a été établie par H. Eyring, M. Polanyi et M. G. Evans en 1935.
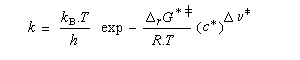

Notons que l'enthalpie libre d'activation de référence n'est pas une grandeur standard car la concentration de référence (1 mol.L-1) ne correspond pas à l'état standard (solution infiniment diluée).
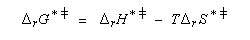
Prenons l'exemple de la réaction de substitution nucléophile bimoléculaire représentée par le schéma suivant.
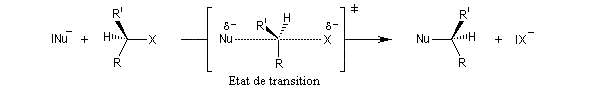
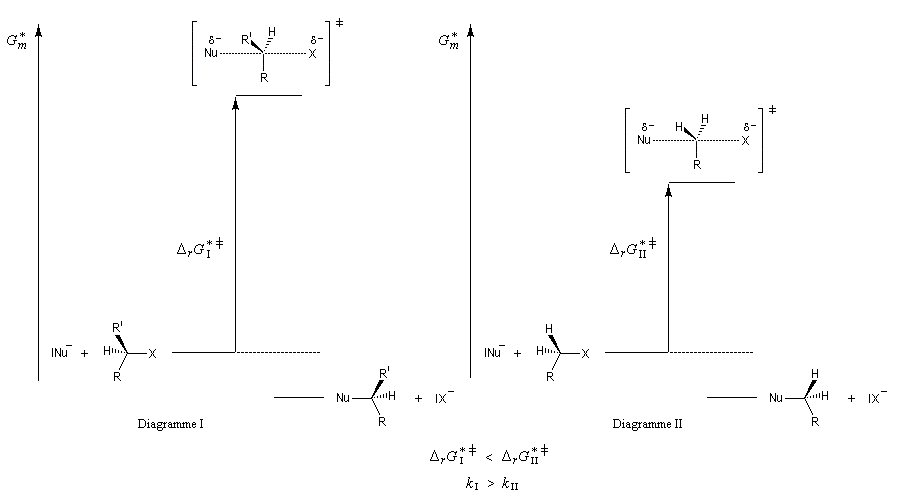
Notons que ce type de diagramme ne donne pas d'information directement sur la vitesse de la réaction car celle-ci dépend également des concentrations des réactifs.
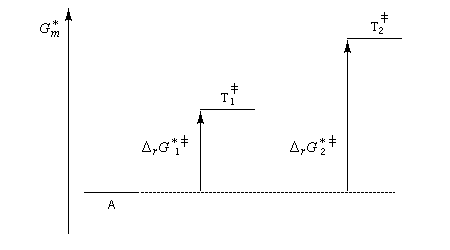
Postulat de Hammond
La connaissance de l'état de transition et de son énergie lors du déroulement d'une réaction sont naturellement d'un grand intérêt notamment lorsqu'il s'agit de l'étape déterminante d'une réaction cinétiquement contrôlée. Malheureusement, un état de transition correspond à
une association transitoire d'atomes qui se traduit par un maximum d'énergie. La durée de vie de cette association est tellement courte qu'on ne peut en faire l'étude qu'avec des méthodes très sophistiquées dans des cas peu nombreux. Il est raisonnable d'admettre, dans certains cas du moins, qu'il est possible de ramener l'étude de la structure et de l'énergie d'un état de transition à celle d'une véritable entité chimique pourvu que leurs énergies soient assez proches. C'est l'objet du postulat énoncé par le chimiste américain G. S. Hammond qui peut s'énoncer de la façon suivante [53] :
|
|
|
|
Etat de transition précoce (faible enthalpie libre d'activation). L'état de transition "ressemble" au réactif |
Etat de transition tardif (grande enthalpie libre d'activation). L'état de transition "ressemble" au produit. |
Un corollaire direct du postulat de Hammond, implique que tout facteur qui abaisse l'énergie d'une entité abaisse du même coup celle de l'état de transition qui lui est le plus proche. Examinons le cas d'un état de transition tardif, conduisant à un intermédiaire I, par exemple un carbocation. Tout facteur abaissant l'énergie de ce dernier doit entraîner ipso facto un abaissement de l'énergie de l'état de transition antécédent.
|
|
|
Sous l'influence d'un facteur stabilisant l'intermédiaire I, l'énergie de l'état de transition qui conduit à cet intermédiaire est abaissée. |
Cette propriété fondamentale est utilisée, par exemple, pour rationaliser la cinétique et la régiosélectivité de la bromation des composés aromatiques ainsi que d'autres substitutions électrophiles du même type dans cette série.
Définitions
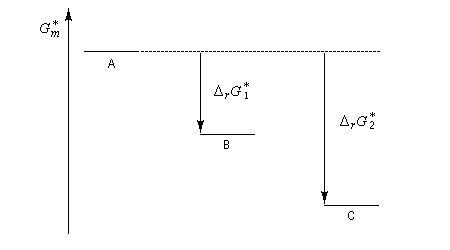
Pour illustrer ces notions nous allons raisonner sur un système particulier. Un réactif A est impliqué dans deux réactions jumelles qui conduisent à des produits notés B et C. On fait l'hypothèse simplificatrice que les réactions directe et inverse sont d'ordre 1. Il s'agit d'étudier l'abondance relative des produits B et C au bout d'une certaine durée de réaction.
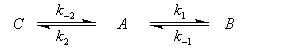
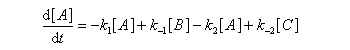
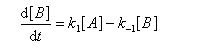
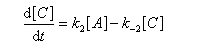
Ce système d'équations peut être simplifié dans deux situations extrêmes.
Contrôle cinétique Le rapport des concentrations des produits formés au début de la réaction est égal au rapport des constantes de vitesses. Le produit majoritaire est le produit formé le plus rapidement. On dit que la réaction est sous contrôle cinétique. La proportion des produits formés en cours de réaction fait intervenir la valeur relative des enthalpies libres molaires d'activation. Sous contrôle cinétique, le produit le plus abondant est celui qui se forme le plus rapidement. Le rapport des concentrations des produits formés à la fin dela transformation est égal au rapport des constantes thermodynamiques. On dit que la réaction est sous contrôle thermodynamique. Le produit formé majoritairement à l'état final est le plus stable. Sous contrôle thermodynamique, le produit le plus abondant est celui qui est le plus stable.
Au début de la transformation, les concentrations des produits B et C sont beaucoup plus faibles que la concentration de A. Il est possible de faire les approximations suivantes :
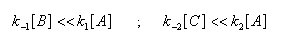
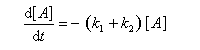
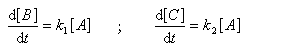
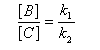
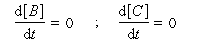
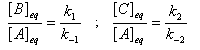
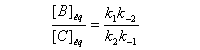
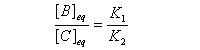
Exemples de réactions sous contrôle thermodynamique :
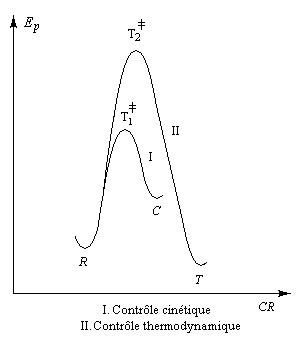
En chimie organique, on fait souvent appel aux diagrammes représentant l'énergie potentielle en fonction de la coordonnée de réaction (CR). On se place alors à l'échelle microscopique. Le diagramme ci-dessous illustre les deux types de contrôles à partir d'un même réactif R.
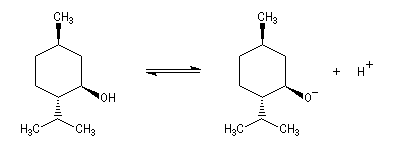
Définition de Lewis Les méthodes électrochimiques ne permettent de faire des mesures que dans une fenêtre de pKa assez étroite en chimie organique. D'autres méthodes doivent être employées. Le couple menthol-ion mentholate peut être mis à profit pour déterminer les pKa des couples acido-basiques comme alternative aux méthodes électrochimiques car les pouvoirs rotatoires spécifiques de l'alcool et de son sel sont très différents. Les organolithiens sont des bases très fortes permettant de déprotoner les hydrocarbures. Superacides On voit que H0 généralise la notion de pH dans ce type de milieu.
Un complexe acide-base de Lewis, encore appelé adduit, est le produit de la réaction entre un acide de Lewis et une base de Lewis.
Soit une réaction entre un acide de Lewis symbolisé par A et une base de Lewis symbolisée par B conduisant à la formation d'un adduit que nous noterons AB.
![]()
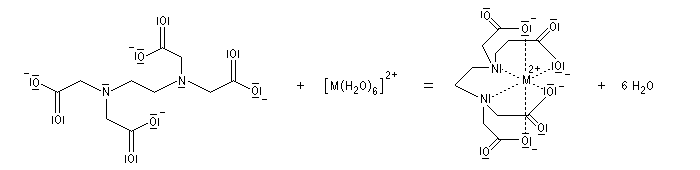
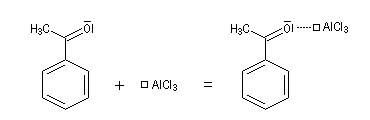
Un autre exemple classique est la formation des énolates par action d'une base sur un composé carbonylé.
L'acide le plus fort pouvant exister dans l'eau est l'ion H3O+ (aq). Tout acide intrinsèquement plus fort protone l'eau pour fournir
H3O+ (aq). Dans les années 60, R. J. Gillespie a proposé d'appeler superacides des acides plus forts que l'acide sulfurique pur. Naturellement, une telle définition comporte une part d'arbitraire. Pour aller plus loin, il faut définir une nouvelle échelle d'acidité en milieu non aqueux. L'échelle d'acidité la plus connue est celle de Hammett (Hammett et Deyrup 1930). On utilise une base de référence notée B ci-dessous. Hammett utilisait la nitroaniline. Le rapport des activités de BH+ et B est déterminé par
des méthodes spectroscopiques (UV, RMN etc.) Dans cette échelle, l'acide sulfurique concentré est caractérisé par une valeur H0 = - 12.
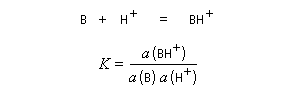
![]()
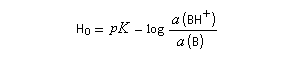
Le mélange équimolaire de HSO3F et de SbF5, découvert dans le laboratoire de G. Olah, a été appelé "acide magique" après qu'un chercheur ait observé la dissolution de la paraffine provenant d'un morceau de bougie tombé par hasard dans le mélange [40]. Il est caractérisé par : H0 = - 19,2.
L'acide fluoroantimonique (HF, SbF5) a une valeur H0 = - 31,3.
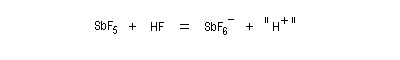
Un tel acide est capable de protoner un hydrocarbure avec formation d'un ion carbonium (I) pentacoordiné puis d'un ion carbénium (II).

Préparation d'un dérivé du cation norbornyle (Laube 1986)

Les milieux superacides ne sont pas seulement des curiosités de laboratoire.
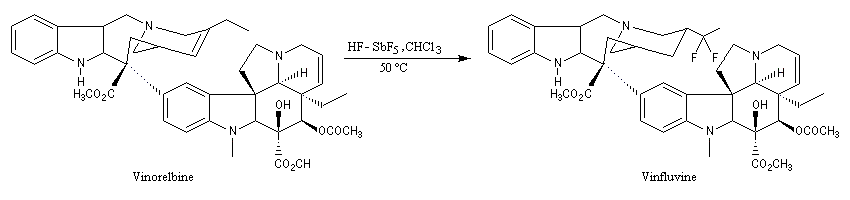
La vinfluvine, un antitumoral, qui fait actuellement l'objet d'essais cliniques, est préparé par fluoration de la vinorelbine en milieu superacide. Le carbocation formé à partir du trichlorométhane arrache un proton du substrat ce qui permet la fixation du fluor.
Basicité et nucléophilie
Une propriété importante d'une base de Lewis est sa nucléophilie. La nucléophilie d'une espèce est une grandeur permettant la comparaison des vitesses relatives de réactions vis à vis d'un même substrat.
Il s'agit donc d'une grandeur cinétique relative permettant de classer les nucléophiles selon la vitesse avec laquelle ils transfèrent leur doublet au substrat. La réaction servant de référence est la suivante.
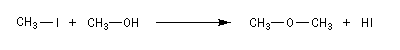
|
Nucléophile |
pKa (HX/X-) |
log k/kr |
Vitesse relative |
|
CH3OH |
-3 |
0 |
1 |
|
F- |
3,4 |
2,7 |
500 |
|
Cl- |
-5,7 |
4,4 |
2,35´104 |
|
Br- |
-7,7 |
5,8 |
6,0´105 |
|
I- |
-5,2 |
7,4 |
2,6´107 |
Parmi les bases non nucléophiles permettant de promouvoir des éliminations E2 citons les amines tertiaires : DBN, DBU, DABCO.
Lorsqu'on recherche une plus grande force, on peut faire appel aux amidures.
Certains nucléophiles possèdent plusieurs points d'attaque. Ainsi, l'ion nitrite peut conduire par substitution nucléophile sur un dérivé halogéné à des dérivés nitro ou nitrito.
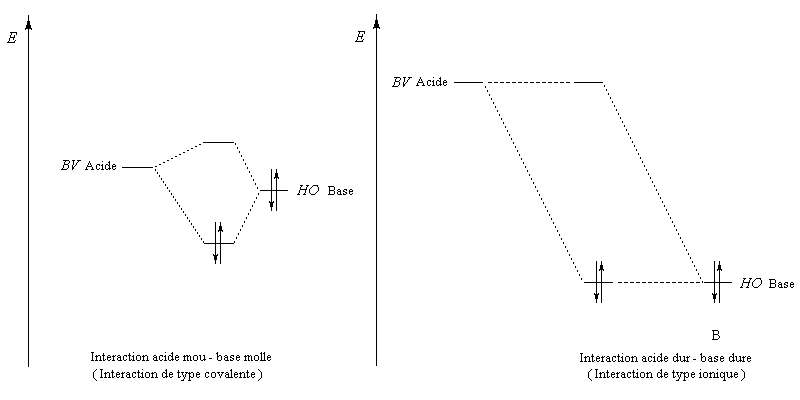
Dureté et mollesse Principe HSAB de Pearson
Le principe HSAB acronyme de Hard Soft Acid Base principle (en français : principe des acides et bases durs et mous) a été introduit par le chimiste américain Ralph G. Pearson en 1963. Afin de rationaliser un certain nombre de faits expérimentaux [59], [60], [61].
Cet auteur distingue trois catégories d'acides et de bases de Lewis : les durs (hard), les mous (soft) et une catégorie intermédiaire (borderline).
Les résultats expérimentaux permettent de dresser un tableau selon les critères ci-dessus :
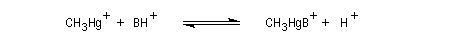
|
durs |
intermédiaires |
mous |
|
H+, Li+, Na+, K+, Mg2+, Al3+, Ce3+, AlCl3, RCO+ |
Fe2+, Co2+, Cu2+, Zn2+, Sn2+, R3C+, SO2 |
Cu+, Ag+, Au+, Hg2+,CH3Hg+ , Pd2+, Pt2+, Br+, I+ |
|
dures |
intermédiaires |
molles |
|
OH-, RO- , F- , Cl-, AcO-, RO- |
ArNH2, C5H5N, N3-, Br- |
H-, R-, I- , R3P, C6H6, C2H4, CN-, SCN-, R2S, RSH, RS-, SO32- |
Exemple:
![]()
![]()
Le principe HSAB présente le grand intérêt de permettre la prévision de réactions à partir de données purement qualitatives cependant les notions de dureté et de mollesse peuvent recevoir une interprétation plus quantitative.
La formation du complexe suivant s'interprète par l'interaction entre le composé éthylénique qui est une base molle et Ag+ qui est un acide mou.
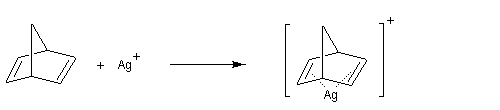
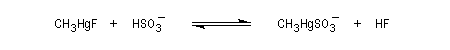
Exemple 2 : l'équilibre suivant est déplacé vers la droite.
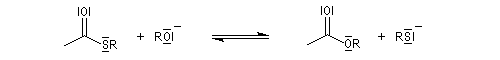
L'ion nitrite est un nucléophile ambident. En effet, il possède deux atomes nucléophiles : l'atome d'azote et l'atome d'oxygène. Sa structure peut être décrite par la méthode de la mésomérie.
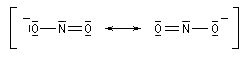
Considérons les réactions de substitutions nucléophiles sur un même dérivé halogéné avec l'ion nitrite comme nucléophile. Dans la réaction (1), l'atome de carbone du dérivé halogéné se comporte comme un site mou ; il réagit avec l'atome d'azote du nitrite.
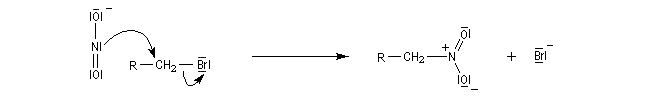
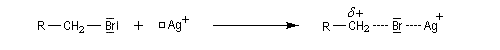

Les ion énolate sont des nucléophiles ambidents. L'atome d'oxygène négatif est dur tandis que l'atome de carbone négatif est mou.
La réaction avec l'iodure de méthyle conduit à une C-alkylation (interaction acide mou-base molle).
En revanche,avec le chlorure de triméthylsilyle, on obtient une O-alkylation (interaction acide dur-base dure).
Notons que cela permet de piéger les énolates sous forme d'éthers d'énols silylés, intermédiaires très utiles en synthèse organique.
La mollesse absolue S est définie comme l'inverse de la dureté absolue.
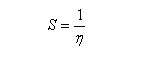
|
molécule |
dureté h (eV) |
|
R2CO RSH R2S RNH2 R2NH R3N PhNH2 Py (pyridine) RCN R3P RF RCl RBr RI |
18,8 9,94 9,87 14,7 14,3 14,0 12,1 15,0 15,9 9,42 45,3 10,9 9,54 8,14 |
Pour un résumé sur le principe HSAB : [34]
Tableau de duretés absolues : [65].
Electronégativité et dureté absolues
En se plaçant dans le cadre d'une approximation de différences finies, les énergies correspondantes se calculent grâce au développement vu plus haut : On en déduit les expressions de I et A respectivement :
Considérons une entité (atome, molécule, ..) d'énergie E comportant N électrons, de charge nucléaire Z. On envisage une variation dN = N- Z du nombre d'électrons. Pour utiliser les méthodes du calcul différentiel on fait l'hypothèse que E est une fonction continue de N.
En effectuant un développement limité de E en fonction de N, on obtient :
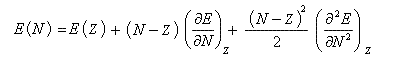
Désignons par I l'énergie d'ionisation et par A l'affinité électronique (opposée de l'énergie de fixation électronique.)
Appliquons les définitions de I et A respectivement.
![]()
![]()
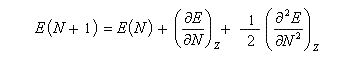
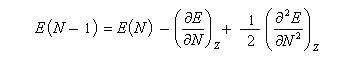
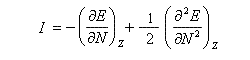
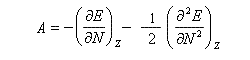
En 1961, R. P. Iczkowsky et J. L. Margrave on proposé de définir l'électronégativité absolue d'une entité (atome, molécule, ion) par la relation [64] :
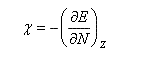
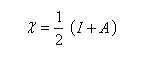
Selon les idées de Parr et Pearson, la dureté est définie par :
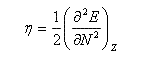
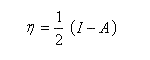
Là encore cette formule permet le calcul de la dureté à partir de données expérimentales (on notera que la dureté s'exprime en eV.)
On en déduit une relation importante entre l'électronégativité absolue et la dureté absolue :
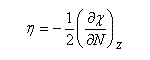
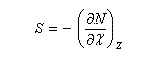
Pour aller plus loin, et examiner les conséquences pratiques des formules précédentes, il est intéressant d'avoir une idée de la manière dont l'énergie E du système dépend du nombre N d'électrons (notons que E < 0.) L'expérience montre que la variation de l'énergie du système en fonction de N, au voisinage de N = Z, a l'allure suivante.
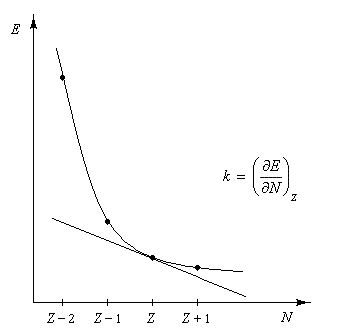
Autrement dit, la courbe qui s'approche le mieux de la courbe expérimentale dessinée plus haut peut être approximée par une portion de parabole. Les coefficients a et b sont des paramètres qui dépendent naturellement du système. Avec cette forme mathématique de l'énergie, l'expression de l'électronégativité du système peut être facilement obtenue en dérivant une fois E par rapport à N
Notons que l'électronégativité est une fonction de N. L'électronégativité du système sans charge excédentaire est la valeur particulière obtenue pour N = Z. C'est une constante.
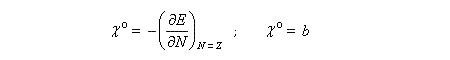
La dureté est obtenue en dérivant deux fois E. Dans le cadre de ce modèle, c'est une constante.
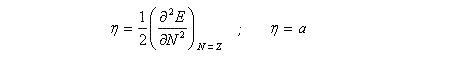
L'électronégativité et la dureté du système sont reliées par la formule suivante.
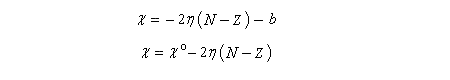
On note l'analogie entre cette dernière expression et celle d'un potentiel chimique. C'est la raison pour laquelle m = - c est appelé potentiel chimique électronique (on verra plus loin que cette analogie thermodynamique s'est montrée très féconde.) Avec ces nouvelles grandeurs, on peut réécrire l'énergie du système sous la forme :
A ce stade nous allons appliquer un principe très général, énoncé pour la première fois par Sanderson en 1951 : le principe d'égalisation des électronégativités [72].
Il consiste à admettre que l'équilibre est réalisé lorsque les électronégativités des deux fragments seront égales dans la nouvelle entité formée.
Avant l'interaction, les électronégativités des fragments A et B valent :
Au cours de la transformation, l'une va diminuer tandis que l'autre va augmenter.
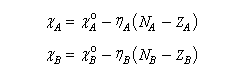
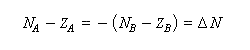
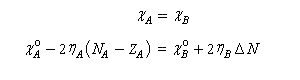
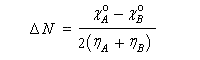
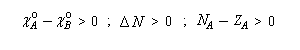
Par ailleurs, comme le fait remarquer Pearson du fait de sa présence au dénominateur, la dureté apparaît comme une "résistance" au transfert électronique entre les espèces [67] (analogie électrique.)
Toujours dans le cadre du modèle précédent, calculons à présent la variation d'énergie du système constitué de l'ensemble A et B.
L'énergie du sous-système A s'écrit :
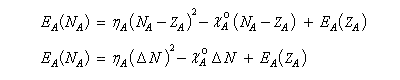
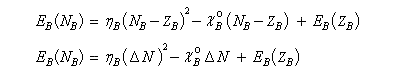
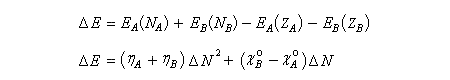
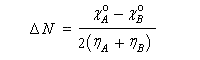
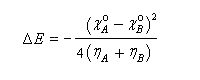
Les résultats précédents peuvent être généralisés dans le cadre des théories de la fonctionnelle de densité (DFT.)
Voir : [22]
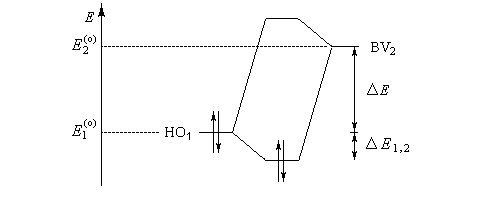
Théorie HSAB et théorie des OM Le théorème de Koopmans relie l'énergie des orbitales moléculaires (dans l'approximation de Hartree-Fock) à l'opposé de l'énergie d'ionisation correspondant à l'arrachement de l'électron occupant cette orbitale. Dans le cadre de cette approximation, les énergies des orbitales frontières sont donc respectivement :
En 1968, Klopman a généralisé et interprété le principe HSAB dans le cadre de l'approximation des orbitales frontières [62].
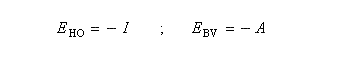
Si l'on revient aux résultats obtenus plus haut pour l'électronégativité et la dureté :
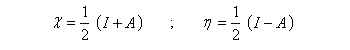
donc :
Le diagramme énergétique ci-dessous résume le calcul précédent.
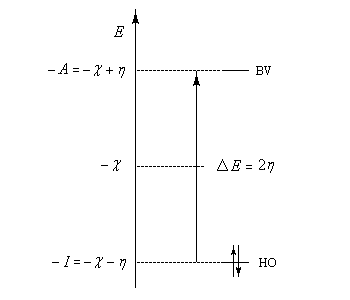
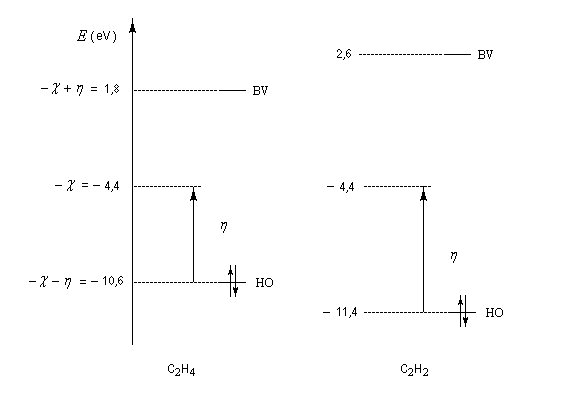
L'électronégativité et la dureté de molécules insaturées et de molécules conjuguées peuvent être calculées au moins de façon approchée au moyen de la méthode de Hückel simple.
Dans le cas de l'éthène les énergies orbitales frontières (niveaux p et p* ) sont respectivement :
Dans ce nouveau cadre, on peut mettre en relation :
|
acides durs (électrophiles) |
acides mous (électrophiles) |
|
|
|
|
bases dures (nucléophiles) |
bases molles (nucléophiles) |
|
|
|
Composé |
CH3-F |
CH3-Cl |
CH3-Br |
CH3-I |
|
c / eV |
3,2 |
3,8 |
4,8 |
4,9 |
|
h / eV |
9,4 |
7,5 |
5,8 |
4,7 |
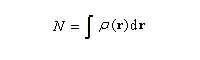
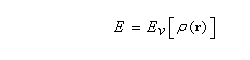
On peut démontrer que dans l'état fondamental la densité électronique exacte r (r) est celle qui rend l’énergie minimale [78].
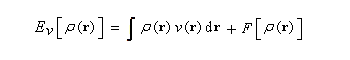
Il existe plusieurs versions des théories basées sur les fonctionnelles de densité électronique. La DFT interprétative (conceptual DFT) constitue un moyen de description de la réactivité chimique pour lequel les notions de potentiel électronique (ou d'électronégativité absolue) et de dureté s'inscrivent assez naturellement et recoivent une interprétation physique.
Comme on l'a vu précédemment, l'électronégativité et la dureté absolue sont des caractéristiques globales d'une entité (atome, molécule, ion.) Pour préciser la réactivité des molécules on a besoin de décrire les propriétés de sites particuliers de celles-ci. En d'autres termes prévoir les zones électrophiles et les zones nucléophiles. La connaissance de la répartition de la densité électronique r (r) qui est une grandeur locale puisqu'elle fait intervenir la position M (r) du point où on la calcule, est naturellement d'une très grande importance.
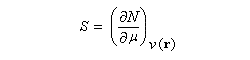
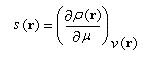
:
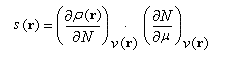
On appelle fonction de Fukui (FF) du système, la quantité :
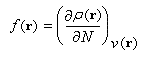
Puisque :
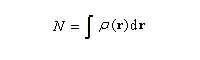
Elle est normalisée.
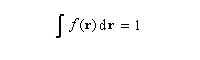
Il s'agit donc du taux de variation de la densité électronique lorsque le nombre d'électrons du système varie. C'est pourquoi cette grandeur constitue un descripteur local des zones électrophiles ou au con traire nucléophiles d'une entité.
En regroupant les relations précédentes, on arrive à :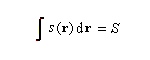
Ce qui indique bien que la fonction de Fukui distribue la mollesse globale de l'entité aux différents endroits de celle-ci.
Compte-tenu du caractère discontinu des variations de N, on est amené à introduire les dérivées à gauche et à droite respectivement. On va donc distinguer deux types de fonctions :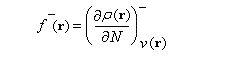
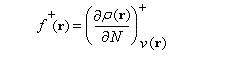
Les fonctions relatives à un atome k constitué d'un système de N électrons, peuvent être calculées à partir de la densité électronique rN,v du système de même géométrie mais possédant respectivement N - 1 ou N + 1 électrons en utilisant l'approximation des différences finies (géométriquement cela revient à confondre la tangente en N à la courbe rN,v (N) avec la sécante quand on passe de N - 1 à N).
si l'on enlève un électron :
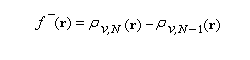
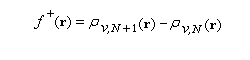
De même, l'attaque par un réactif nucléophile va avoir lieu là ou f +(r) est élevée car c'est au niveau d'un tel site que la stabilisation des électrons additionnels est la plus grande.
On définit un descripteur de réactivité pour une attaque radicalaire comme la moyenne des descripteurs précédents :
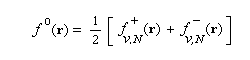
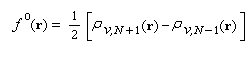
Désignons par ji (r) la ième OM et par ni le nombre d'électrons décrit par cette OM. La densité électronique s'obtient en sommant sur les OM.
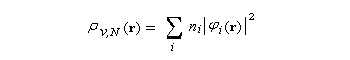
Les fonctions de Fukui définies plus haut sont obtenues par dérivation.
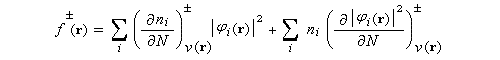
En général, l'hypothèse faite est que les électrons quittent l'orbitale occupée la plus haute en énergie. Donc :
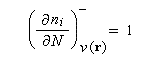
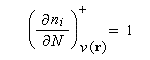
Avec ces approximations, les fonctions de Fukui, s'identifient avec la densité électronique orbitales frontières HO et BV respectivement.
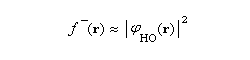
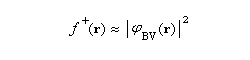
On trouvera à la référence [39], des compléments sur les principales propriétés des fonctions de Fukui.
Bibliographie
[1] F. A. Carey, R. S. Sunberg - Advanced Organic Chemistry, Fifth Edition, 2007, SpringerVous pouvez, si vous le souhaitez, utiliser le contenu de cette page dans un but pédagogique et non commercial.
Texte, dessins, photographies : Gérard Dupuis - Lycée Faidherbe de LILLE
mai 2014